Написать уравнение параболы, касающейся оси абсцисс в точке (3; 0) и оси ординат в точке (0; 5)

👇

Ответ:

Гульшат11111111

16.03.2022

Парабола не может касаться оси у. Очевидно, речь идет о точке пересечения с осью у.
Уравнение параболы в общем виде:
y=a(x+b)²+c
b и c показывают сдвиг параболы ax² по оси х и у соответственно.
Раз парабола касается оси х в точке (3,0), значит, в этой точке лежит ее вершина, т.е. парабола по оси у не сдвинута - следовательно, c=0.
А по оси х парабола сдвинута на 3. Следовательно, b=-3
y=a(x-3)²
Координаты данных точек должны удовлетворять уравнению параболы. Подставляя, находим а:
5=a(0-3)²
5=9a
a=5/9
Уравнение параболы имеет вид:
$y= \frac{5}{9}(x-3)^2$

4,8(8 оценок)

Открыть все ответы

Ответ:

Znanija96

16.03.2022

Прямые ab и cd не являются параллельными.

Объяснение:

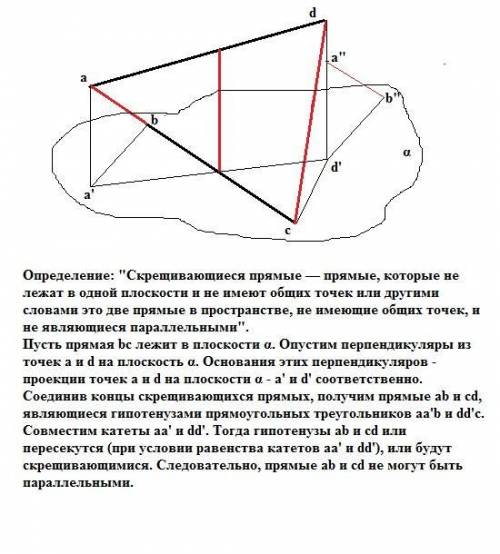
Определение: "Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными".

Пусть прямая bc лежит в плоскости α. Опустим перпендикуляры из точек a и d на плоскость α. Основания этих перпендикуляров - проекции точек а и d на плоскости α - a' и d' соответственно. Соединив концы скрещивающихся прямых, получим прямые ab и cd, являющиеся гипотенузами прямоугольных треугольников aa'b и dd'c. Совместим катеты aa' и dd'. Тогда гипотенузы ab и cd или пересекутся (при условии равенства катетов aa' и dd'), или будут скрещивающимися. Следовательно, прямые ab и cd не могут быть параллельными.

Являются ли прямые ab и cd параллельными,если ad и bc - скрещивающиеся прямые?

4,8(23 оценок)

Ответ:

dalldall

16.03.2022

В начале построим рисунок, который приложу вложением. Для наглядности соединим т. О поочерёдно с точками A, B, C, D. Получаем пирамиду с вершиной в т. O, в основании которой лежит квадрат ABCD.
Первый вопрос: 1). Докажем, что плоскость ABCD параллельна плоскости A1B1C1D1. Для этого построим пары диагоналей AC, BD, а также A1C1, B1D1.
2). Теперь рассмотрим треугольник OBD. Прямая B1D1 параллельна прямой BD, как средняя линия треугольника OBD, т.к. B1D1 соединяет середины его сторон B1 и D1 (эти точки середины по условию).
3). Теперь рассмотрим треугольник OAC. Прямая A1C1 параллельна прямой AC, как средняя линия треугольника OAC, т.к. A1C1 соединяет середины его сторон A1 и C1 (эти точки середины по условию).
4). Тогда получаем, что две пересекающиеся прямые AC и BD плоскости ABCD параллельны двум пересекающимся прямым A1C1 и B1D1 плоскости A1B1C1D1, а из этого, по теореме о параллельности двух плоскостей, следует, что плоскости ABCD и A1B1C1D1 параллельны, что и требовалось доказать.
Второй вопрос: 1). Рассмотрим треугольник OBA. B1A1 - средняя линия треугольника OBA, т.к. соединяет середины сторон OB и OA (B1 и D1 середины по условию). Тогда B1A1=1/2 AB=10/2=5.
2). Аналогично B1C1 - средняя линия треугольника BC, C1D1 - средняя линия треугольника CD, A1D1 - средняя линия треугольника AD.
3). Тогда, B1C1=5, C1D1=5, A1D1=5.
4). Периметр A1B1C1D1=B1C1+C1D1+A1D1+B1A1=5+5+5+5=20

Квадраь abcd со стороной 10 см и точка o не лежат в одной плоскости точки a1b1c1d1 являются середина