Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
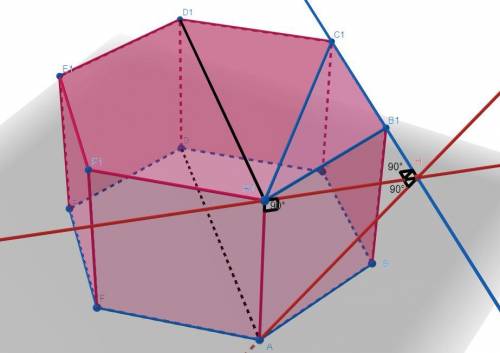
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
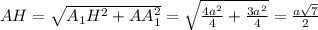
ответ: 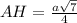
Рассмотрим треугольник АВД ( можно и АСД, т.к. они равны).
АО - биссектриса этого треугольника.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Следовательно, АВ:АД=ВО:ОД=5:13
Пусть коэффициент отношения сторон будет х.
Тогда АВ=5х,
АД=13 х.
Угол АСВ равен уголу САД как накрестлежащий.
Но угол САД равен углу САВ по условию.
Отсюда углы ВАС и ВСА равны, и треугольник АВС равнобедренный. АВ=ВС
Опустим высоту ВН.
Высота равнобедренной трапеции делит большее основание на отрезки, из который меньший равен полуразности оснований, а больший- их полусумме.
АН=(АД-ВС):2=4х
АВ=ВС=5х
Налицо «египетский» треугольник, и ВН равно 3х, и х=30. (Можно проверить по т. Пифагора)
Тогда 3х=90, х=30 cм=3 дм
АД=390см=39 дм
, ВС=150=15 дм
Высоту ВН выразим в дм. ВН=9 дм
Площадь трапеции находим по классической формуле
S=h*(a+b):2
S=9(15+39):2=243 дм ² ( или 24300 см ² )
------
[email protected]