сумма углов треугольника равна 180, а напротив одинаковых сторон в треугольнике лежат равные углы. Так как углы равны и их 3, то 3х = 180, х=60
Или
если мы построим высоту из одного из углов, то высота поделит сторону пополам. Допустим сторона равна А, тогда у нас 2 треугольника со сторонами А, А/2 и еще одной. Мы знаем, что напротив угла в 30% в прямоугольном треугольнике лежит катет, равный 1/2 гипотенузы. А А/2 в 2 раза меньше чем А, соответсвенно угол равен 30. Из чего следует, что противоположный угол равен 60 (прямоуг. треуг.). Также и со вторым треуг. 2 угла по 60 градусов, значит последний тоже 60
Для приведенного квадратного уравнения x^2 +px +q =0
Теорема Виета: x1+x2 = -p ; x1x2 =q
Формула корней: x1,2 = -p/2 +-√[(p/2)^2 -q]
--------------------------------------------------------------- -
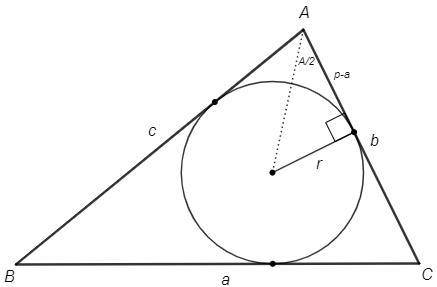
По теореме котангенсов (p - полупериметр)
ctg(A/2) =(p-a)/r => p =r*ctg(A/2) +a
b+c =2p-a
S =pr =1/2 bc sinA => bc =2pr/sinA
Мы нашли сумму и произведение искомых величин (b, c).
По теореме Виета эти величины являются корнями квадратного уравнения
x^2 -(2p-a)x +2pr/sinA =0
По формуле корней квадратного уравнения
b,c =p -a/2 +-√[(p -a/2)^2 -2pr/sinA], где p =r*ctg(A/2) +a