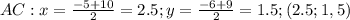

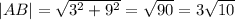
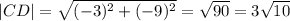
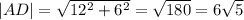
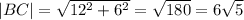
АВСD- квадрат.
О - центр нижнего основания цилиндра, в который вписан квадрат. О1- центр верхнего основания.
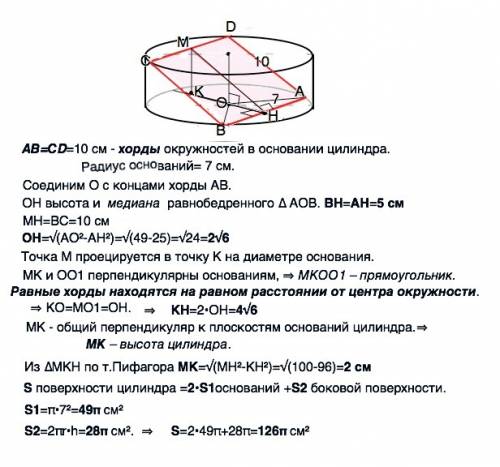
АВ=СD=10 см - хорды окружностей в основании цилиндра.
Радиус оснований= 7 см.
Соединим О с концами хорды АВ.
Проведем высоту ОН (она же медиана) в равнобедренном ∆ АОВ. ВН=АН=5 см
МН║ВС=10 см – средняя линия АВСD и пересекает ось цилиндра.
ОН=√(AO²-AH²)=√(49-25)=√24=2√6
Точка М проецируется в точку К на диаметре основания.
МК и ОО1 перпендикулярны основаниям, поэтому МКОО1 – прямоугольник.
Равные хорды находятся на равном расстоянии от центра окружности. ⇒КО=МО1=ОН.
КН=2•ОН=4√6
МК - общий перпендикуляр к плоскостям оснований цилиндра.⇒
МК – высота цилиндра.
Из ∆МКН по т.Пифагора МК=√(МН²-КН²)=√(100-96)=2 см
S поверхности цилиндра =2•S1оснований +S2 боковой поверхности.
S1=π•7²=49π см²
S2=2πr•h=28π см².
S=2•49π+28π=126π см²
b{-2;0;4}⇒-1/2b{1;0;-2}
p=3a-1/2b⇒p{4;-6;-2}
c{8;m;n}=kp
4k=8⇒k=2
m=2*(-6)=-12
n=2*(-2)=-4
c{-8;-12;-4}