Пусть имеем ромб ABCD, т.O - точка пересечения диагоналей, KO- перпендикуляр плоскости ромба
Рассмотрим прямоугольный треугольник AOD.
AD=46
3*OD=4AO
Пусть x - коэффициент пропорциональности,тогда
AC=4x
OD=3x
(AO)^2+(OD)^2=(AD)^2
(4x)^2+(3x)^2=(45)^2
16x^2+9x^2=2025
25x^2=2025
x^2=81
x=9
то есть
AO=4*9=36
OD=3*9=27
Из треугольника OKD:
(KD)^2=(OD)^2+(OK)^2
(KD)^2=729+1296=2025
KD=45
Из треугольника OKA
(AK)^2=(AO)^2+(KO)^2
(AK)^2=1296+1296=2596
AK=36*sqrt(2)
то есть
KD=KB=45
KA=KC=36*sqrt(2)
Дано:а=2 сторона квадрата, АВС правильный треугольник.
Найти: Sавс.
Решение:Д диагональ квадрата.
По теореме Пифагора Д^2 = а^2 + а^2
Д=кор.кв.( 2 х а^2) = а х кор.кв.2= 2 х кор.кв.2
Д является диаметром описанной окружности около квадрата.
Следовательно радиус окружности r=1/2 х Д = кор.кв.2
Радиус окружности вписанной в правильный многоугольник находится по формуле:
r = А / (2 х tg(180/n)) , где А сторона многоугольника , n угол многоугольника.
r = А / (2 х tg(180/60)) = А /6 х ( кор.кв.3 )
А = (6 х r) / ( кор.кв.3) = (6 х ( кор.кв.2) ) / ( кор.кв.3)
Sавс = А х H / 2 , H высота правильного треугольника.
По теореме Пифагора А ^2 = (А / 2) ^2 + H^2
H ^2 = А ^2 - (А / 2) ^2 = 3 х А ^2 / 4
H =( кор. кв. 3 х А) / 2
Sавс = А х H / 2 = Sавс =( А / 2) х ( кор. кв. 3 х А) / 2 = ( кор. кв. 3 х А ^2 ) / 4 = (36 х 2 х ( кор. кв. 3 )) /( 3 х 4) = 6 х ( кор. кв. 3 )
ответ: Sавс = 6 х ( кор. кв. 3 )
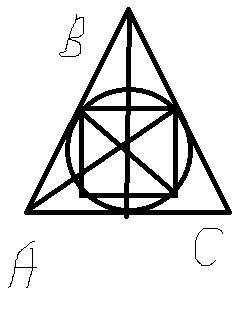
Для правильного построения любого чертежа можно располагать заданные линии произвольно на листе. Необходимо только соблюдать пропорции указанные в задании, зная свойства прямых и плоскостей. Итак,спроецируем отрезок АВ на горизонтальную плоскость. Проекция этой плоскости представляет собой прямую параллельную оси Х. Для удобства построения примем ось Х за проекцию этой плоскости. Затем под некоторым углом пересечём ось Х отрезком АВ. Точка А расположится ниже оси Х , точка В выше. Опустим перпендикуляры на ось Х АА1=3, и ВВ1=5. Из точки А1 проведём линию параллельную АВ до пересечения её с продолжением перпендикуляра В1В в точке В2. Получим параллелограмм, так как его стороны попарно параллельны. Значит АА1=ВВ2. ТогдаВ1В2=5+3=8. АВ=А1В2 и они параллельны поэтому их проекции равны. Значит А1В1(прекцияАВ)=корень из(А1В2квадрат-В1В2квадрат)=кор. из(100-64)=6
AВСD - ромб. SO - перпендикуляр к его плоскости. SO = 36. AB=BC=CD=AD=45
Найти: SA = SC = ? и SD = SB = ?
Тр.AOD - прямоуг. ( по свойству диагоналей ромба). Так как диагонали (а значит и их половины) относятся как 4:3, обозначим 1 часть в этой пропорции за х. Тогда:
(4х)кв + (3х)кв = 45 кв 25х кв = 45 кв. 5х = 45 х = 9
Тогда АО = 4х = 36. DO= 3х = 27.
Из тр-ка SAO: SA = кор(АО кв + SO кв) = 36кор2.
Из тр-ка SDO: SD = кор(OD кв + SO кв) = кор(27 кв + 36 кв) = кор2025 = 45.
ответ: 45; 36кор2; 45; 36кор2.