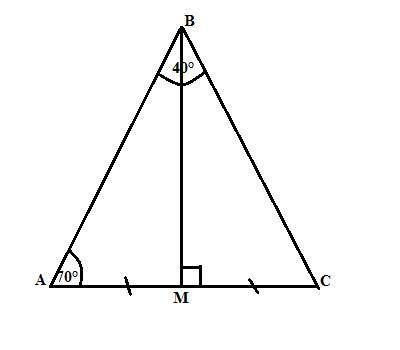
∠МВС = 20°.
∠ВСМ = 70°.
Объяснение:
В треугольнике АВС отрезок ВМ является и высотой (∠ВМА = 90° - дано) и медианой (точка М - середиеа стороны АС - дано). Следовательно, треугольник АВС равнобедренный с основанием АС и отрезок ВМ является биссектрисой (свойство). Тогда
∠МВС = ∠АВС:2 = 40:2 = 20°.
∠ВСМ = ∠ ВАМ = 70° (углы при основании равнобедренного треугольника).
Или так:
∠ВМА=∠ВМС=90° как смежные, равные в сумме 180°.
Прямоугольные треугольники АВМ и СВМ равны по двум катетам: ВМ - общий, а АМ = СМ (так как точка М - середина стороны АС - дано) Из равенства треугольников имеем равенство углов, лежащих против равных сторон:
∠МВС = ∠МВА = ∠АВС:2 = 40:2 = 20°. (∠АВС = ∠МВС + ∠МВА)
∠ВСМ = ∠ ВАМ = 70°.
Пусть АВ = х, тогда ВС = х + 4.
По теореме косинусов составим уравнение:
AC² = AB² + BC² - 2AB·BC·cos∠B
14² = x² + (x + 4)² - 2 · x · (x + 4) · cos120°
196 = x² + x² + 8x + 16 - 2x(x + 4) · (- 1/2)
196 = 2x² + 8x + 16 + x² + 4x
3x² + 12x - 180 = 0
x² + 4x - 60 = 0
D = 16 + 240 = 256
x = (- 4 + 16) / 2 = 6 x = (- 4 - 16) / 2 = - 10 не подходит по смыслу
АВ = 6 см,
ВС = 6 + 4 = 10 см
Р = 6 + 10 + 14 = 30 см