№1
0,25
№2
81x⁴-108x³√6+324x²-72x√6+36
№3
10
Пошаговое объяснение:
№1
0,5sin(-1650°)=-0,5sin(4*360°+210°)=-0,5sin(210°)=-0,5sin(180°+30°)=-0,5sin(-30°)=0,5*sin(30°) =0,5*0,5=0,25
№2
найдем коэффициенты бинома Ньютона из треугольника Паскаля (смотри картинку). Так как у нас 4-я степень, то коэффициенты будут 1,4,6,4,1
Получаем формулу (x+y)⁴=x⁴+4x³y+6x²y²+4xy³+y⁴
у нас x=√6, y=-3x
(√6-3x)⁴=(√6)⁴+4(√6)³*(-3x)+6(√6)²(-3x)²+4(√6)(-3x)³+(-3x)⁴=36-4*6√6*3x+6*6*9x²-4√6*27x³+81x⁴= 36-72x√6+324x²-108x³√6+81x⁴
=81x⁴-108x³√6+324x²-72x√6+36
№3
\begin{gathered}\sqrt{12+\sqrt{44} } *\sqrt{12-\sqrt{44} } = \sqrt{(12+\sqrt{44})(12-\sqrt{44}) } =\sqrt{12^2-(\sqrt{44})^2 }=\\ = \sqrt{144-44 }=\sqrt{100} =10\end{gathered}
12+
44
∗
12−
44
=
(12+
44
)(12−
44
)
=
12
2
−(
44
)
2
=
=
144−44
=
100
=10
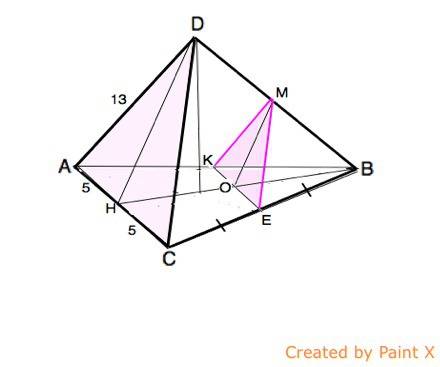
В тетраэдре DABC DA=DC=13, AC=10, E-середина BC. Постройте сечение тетраэдра плоскостью, проходящей через точку E параллельно плоскости ADC, и найдите площадь сечения.
Построение сечения:
Сделаем рисунок тетраэдра.
На середине ВС отметим точку Е.
Проведем ЕК параллельно АС.
На боковых гранях ВСD и ВАD проведем из Е и К параллельно ребрам СD и АD прямые до пересечения на ребре в точке М.
КМ и ЕМ - средние линии ∆ ADB и ∆ CDB
В плоскости КМЕ пересекающиеся прямые КЕ и ЕМ соответственно параллельны пересекающимся прямым АС и DС.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.⇒
плоскость сечения КМЕ || плоскости ADC.
––––––––––––––––
В тетраэдре боковая грань ADC – равнобедренный треугольник по условию. Треугольники КМЕ и АDC подобны, т.к. стороны ∆ МКЕ - средние линии ∆ АВС, ⇒ k=АС:КЕ=2
Высота DН равнобедренного треугольника АDС - его медиана. ⇒ АН=НС=5, ∆ ADH=CDH - прямоугольные.
По т. Пифагора DН=12, но можно обойтись без вычислений, если вспомнить, что стороны треугольника АDН из часто встречающихся в задачах Пифагоровых троек с отношением 13:5:12
Тогда S ∆ ADC=DH•AH=12•5=60
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
S ∆ ADC:S ∆ KME=k²= 4
S ∆ KME=60:4=15 (ед. площади)
Длинна вектора |AB|=sqrt -1^2+-3^2= sqrt 10.
Координаты=x2-x1;y2-y1=-1;3