Дано :
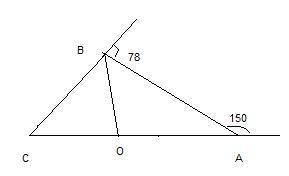
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1) можно найти расстояние между точками Аи В, А и С.
А и В, d= =
= =
=
A и C, d= =
= =
=
т.к. расстояния между точками равны, значит длины сторон равны, а значит треугольник равнобедренный
2) высота равна расстоянию от значения х т.А до значения х т.В или т.С взятых по модулю
высота=|-6|+2=6+2=8
3)уравнение в общем виде: у=kx+b
подставляем в него координаты известных нам точек
уравнение:
у=0.375*х+3,25