Тетраэдр — многогранник, гранями которого являются четыре треугольника.
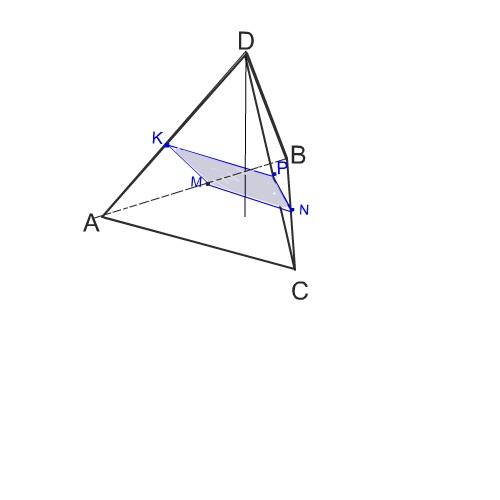
Сечение тетраэдра плоскостью PNM является четырехугольником, стороны которого параллельны друг другу и потому этот четырехугольник - параллелограмм.
В нем MN является средней линией стороны АС и потому отрезок MN параллелен АС , а его длина равна половине АС=5 см
PN вляется средней линией стороны DB, параллелен ей, и длина PN=6 см
КР принадлежит плоскости PNM, параллельна АС т.к. через три точки, не лежащие на одной прямой, можно провести только одну плоскость. В данном случае этими точками являются точки P, N, и M.
КА=РС, и потому точка К - середина ребра АD
Точки М, N и Р - середины сторон DC, AB и BC и потому КМ=РN и К- середина DА
Четырехугольник KPNM - параллелограмм, в нем
PN=KM=6см и
MN=KP=5см
Периметр KPNM=2(6+5)=22 см
Ход решения следующий:
имеем треугольник АВС, высота в котором СН,
нарисовав увидим что АН=12,6 и НВ=22,4
угол АСН=90град-уголСАН
угол АСН=уголАВС
по рисунку видно что треуголиники АВС, АСН, СВН подобны
следует что
СН=12,6*k
СН=22,4/k где k - коэффициент подобия
12,6*k=22,4/k
k=1,34
далее получаем
СН=16,8
AC*AC=16,8*16,8+12,6*12,6
AC=21
CB*CB=AB*AB-AC*AC
CB*CB=35*35+21*21=1225-441
CB=28
стороны все известны