' - обозначение вектора (в моём решении).
а) DB' = DA' + DC' = a' + b' (по правилу параллелограмма).
б) OD' = OC' + CD' =AC'/2 - b' = (AD' + DC')/2 - b' = (-a' + b')/2 -b' = -(b' + a')/2
в) AC' = AD' + DC' = -a' + b'
г) DM' = DC' + CM' = b' + CB' / 2 = b' + DA' / 2 = b' + a'/2

Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть 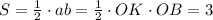 .
.
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда 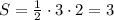 .
.
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой 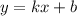 координаты точки А(4,3) и , например, В(2,0), получим:
координаты точки А(4,3) и , например, В(2,0), получим:
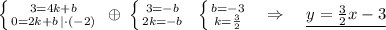
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
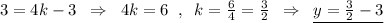
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.
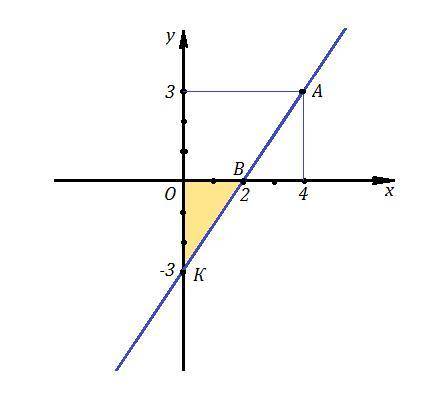
Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть 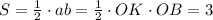 .
.
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда 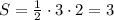 .
.
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой 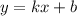 координаты точки А(4,3) и , например, В(2,0), получим:
координаты точки А(4,3) и , например, В(2,0), получим:
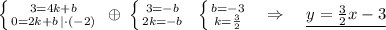
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
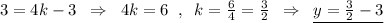
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.

а)
б)
в)
г)