1.Углы альфа и бетта вписанные, значит они равны половине дуги на которую опираются, следовательно дуга соответствующая углу альфа равна 21*2=42(град), а дуга соответствующая углу бетта 49*2=98(град).
Найдем градусную меру дуги соответствующую углу х, 360-(180+98+42)=40, значит угол х=1/2*40=20(град)
ответ: 20град.
2.2х+3х+4х=180
9х=180
х=20
20*2=40(1-ый угол)
20*3=60(2-ой угол)
20*4=80(3-ий угол)
Проверка:
40+60+80=180
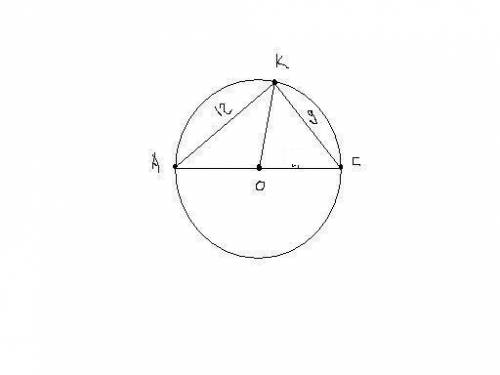
3.В треугольнике АКС угол К-прямой=90 градусов. Т.к Хорды окружности АК и КС построены из одной точки К на концы диаметра. Отсюда по тореме пифагора АС²=АК²+КС²
АС²=12²+9²=225
АС=√225=15
Радиус равен 15/2=7,5 (рисунок внизу)
По условию т.А перемещается в т.В поворотом, значит обе они лежат на одной окружности с центром поворота О' и радиусом О'А=О'В.
Аналогично т.С->т.Д, значит они тоже лежат на одной окружности с ц.п. О'' и радиусом О''С=О''Д.
Поскольку точки А, В, С, Д принадлежат прямоугольнику и являются его вершинами, то они должны лежать на общей описанной окружности с единственным центром О'=О''=О, только тогда одновременно выполняется О'А=О'В==О''С=О''Д
Угол поворота СОД= 180-2*ОСД= 180-2(90-ВСО)=180-2(90-20)=40°
АВСД-ромб
АВ=ВС=СД=ДА=4√3
уг А=120*
ВД>АС - диагонали
1) ВД-?
2) S-?
3) r-?
4) R-?
Решение:
1. АС пересекает ВД в точке О
Рассм треуг АВО,
а) в нем уг А=60* ( тк диаг в ромбе биссектрисы его углов), уг О=90* (т к в ромбе диагонали перпендикулярны), след уг А=30* ( по теореме о сумме углов в треуг).
б) АО=2√3 (по св-ву катета, леж. против угла в 30*)
в) ВО=√(48-12), ВО=√36 , ВО=6 (по теореме Пифагора)
ВД=2*ВО ( по св-ву диагоналей ромба) ВД=12
2. АС=2*АО, АС=4√3 ( по св-ву ромба)
S(ABCD)= 1/2* AC*BD
S(ABCD)= 1/2* 4√3 * 12 = 24√3
3. r=D*d / 4a, где d,D - диагонали ромба (меньшая и большая), а - сторона ромба.
r=4√3 * 12 / 4 * 4√3 = 3
4. Описать окружность около ромба нельзя, только если этот ромб квадрат.