не могу сделать рисунок, поэтому напишу так, думаю разберешься.
пусть пирамида МАБСД, где м-вершина. т.к. основание квадрат, а его периметр 24, из этого находим одну сторону- АД=24:4=6.
бок.поверхность равна 96, значит площадь одного треугольника равна- амд=96:4=24
рассмотрим треугольник амд. он равнобедренный, его площадь 24, сторона ад равна 6. апофема пирамиды это высота боковой грани правильной пирамиды, проведенная из ее вершины. проведем из вершины М перпендикуляр к стороне АД, получаем МО.
АО=6/2=3. высота треуголника АМД(она же апофема пирамиды) равна 24:3=8
ответ 8
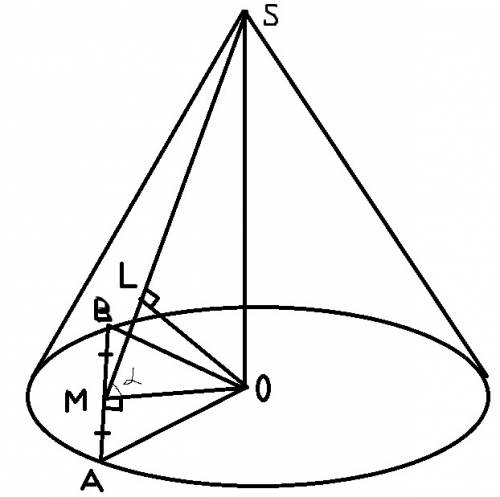
Есть конус. т.О - центр основания, Д - вершина, АВ - хорда.
Рассмотрим равнобедренный треугольник АВО: АО=ВО=r=5, АВ=6. Из т.О опустим перпендикуляр ОС к стороне АВ:
ОС^2=AO^2-AC^2=5^2-(6/2)^2=25-9=16, ОС=4.
Рассмотрим прямоугольный треугольник СДО:
СД^2=OC^2+ОД^2=4^2+12^2=16+144=160, СД=4*корень из 10
Из т.О проведем перпендикуляр ОЕ к стороне СД. Треугольники СДО и ЕДО подобны (угол Д общий, угол СОД=ОЕД=90). Тогда:
СД:ОД=ОС:ОЕ;
ОЕ=ОД*ОС/СД=12*4/(4*корень из 10)=12/корень из 10
пр - параллелограмм
h - высота
a - основание
S тр=(1/2)*h*a
S пр=h*a
следовательно S пр=S тр*2=21*2=42