Итак, нам нужно найти угол между прямой SA и (SBD)?
Давай произведем для начало описание самой задачи(что в ней вообще происходит и какой именно угол нам необходимо найти.
Пусть точка О-является центром основания правильного 4-ехугольника ABCD(квадрата), точка K-середина ребра BS
ΔSOK-является прямоугольным, SO⊥OK,OK⊥(SBD) , т.к OK⊥BC, а BC⊂(SBD),SA⊥(ABCD),SA⊥SC.
Итак, мы выяснили, что SA⊥SC,CK⊥(SBD )⇒ ∠SCK-искомый линейный угол
OK=1/2AB=1/2*1=0,5
SK-высота ΔSBC,то есть SK=√3/2(по формуле равностороннего треугольника)
cos∠SKC=OK/SB=0,5/(√3/2)=1/√3=√3/3
α=arccos√3/3 или
sin∠SKC=SC/KC=√1/3
α=arcsin√1/3
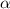- градусная мера сектора, R- радиус окружности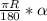 
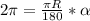
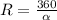
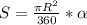
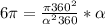
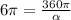
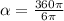
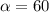
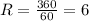
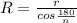
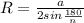
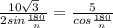
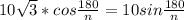
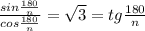
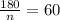, откуда n=3
1) так как диагональ ромба является биссектрисой угла, а угол между диагональю и стороной равен 45 градусов, то весь угол для которго данная диагональ является биссектрисой равен 2 данным углам, т.е. 45 * 2 = 90 градусов, а так как в ромбе две пары равных углов и сумма одной из этой пары равна 90 + 90 = 180 градусов а сумма углов в ромбе равняется 360 градусо то сумма углов другой пары равняется 360 - 180 = 180 градусов а так как в этой паре два равных угла, то каждый угол равен 180/2 = 90 градусов.
Так как дан ромб - то все стороны равны и мы доказали что все углы прямые, следовательно этот ромб-квадрат
2)Так как АЕ- биссектриса угла АВД, то треугольник АВЕ-равнобедренный так как в параллелограмме6 биссектриса отсекает равнобедренный треугольник. следовательно АВ = АЕ, а так как АВ = 7, то и АЕ=7.
ВС = АЕ + ЕС = 7 + 3 = 10
так как АВСД - параллелограмм то АВ = СД и ВС = АД, следовательно АВ = СД = 7 и ВС = АД = 10.
Равсд = АВ + ВС + СД + АД = 2АВ + 2СД = 2* 7 + 2*10 = 14 + 20 = 34 см.
ответ: Равсд = 34 см