16.
а)
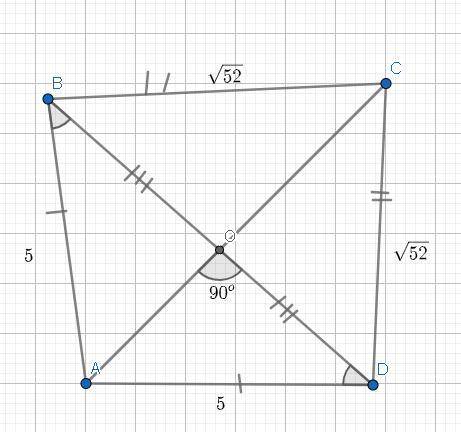
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как: 
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: 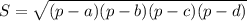
№2
Треугольник КВН-прямоугольный:
По теореме о сумме острых углов прямоугольн. треугольника : 90°-32°=58°-угол КМН.
РАССМОТРИМ треугольник КМТ-прямоугольный:
По теореме о сумме острых углов прямоугольного треугольника : 90°-58°=32°-КНТ.
№3 Рассмотрим треугольник АСВ-прямоугольный:
Угол В=26°,найдем угол А
По теореме о сумме острых углов прямоугольного треугольника :
90°-26°=64°-угол А
АК-биссектриса, высота, медиана и делит угол А пополам.
64°:2=32°-угол САК и угол КАВ.
РАССМОТРИМ треугольник САК-прямоугольный:
По теореме о сумме острых углов прямоугольного треугольника :
90°-32°=58°-УГОЛ АКС.
№9 не знаю)
S=1/2 АС* BD
AC*BD= 24*2=48
Диагональные сечения — прямоугольники АСС1А1 и BDD1B1 с площадями S₁=AC⋅CC₁ и S₂=BD⋅DD₁.
СС₁=DD₁
Тогда
S₁*S₂= AC*CC₁*BD*DD₁=AC*BD*CC₁²
30*40= 48 * CC₁²
CC₁ =√25=5
V= S* CC₁= 24*5=120