1) ∠А=35°, ∠В=90°, ∠С=55°
2)Нет
1) Если описать окружность вокруг ΔАВС, то центр такой окружности будет в точке D. Это прямоугольный треугольник ∠В=90°.
Рассмотрим ΔВDС. Он равнобедренный DВ=DС, значит
∠DВС=∠DСВ, а ∠АDВ- внешний угол ΔВDС
∠АDВ=∠DВС+∠DСВ=2∠DВС
∠DВС=∠АDВ:2=110°:2=55°.
∠С=55°. По теореме о сумме острых углов прямоугольного треугольника ∠А=90°-55°=35°
2)Нет
По теореме о сумме сторон треугольника : сумма длин двух любых сторон треугольника больше длины третьей стороны этого треугольника
22+27 >49
49>49 - не выполняется
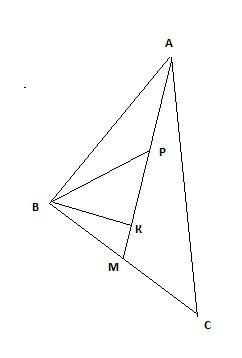
Построим треугольник АВС, площадь которого равна 40 кв. см, Проведем медиану АМ. и обозначим точу Р такую, что АР:РМ=2:3.
Так как медиана треугольника делит его на две равновеликие части, то Sавм=40/2=20 кв. см.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Для наглядности построим высоту ВК – она будет являться высотой как для треугольника ВАМ так и для треугольника ВРМ
Основания Данных треугольников будут соотноситься как 3:5, значит
Sврм : Sвам=3 : 5
Sврм= Sвам*3 / 5=20*3/5=12 кв.см.