дано: δ авс
∠с = 90°
ак - биссектр.
ак = 18 см
км = 9 см
найти: ∠акв
решение.
т.к. расстояние от точки измеряется по перпендикуляру, то опустим его из (·) к на гипотенузу ав и обозначим это расстояние км.
рассмотрим полученный δ акм, т.к. ∠амк = 90°,то ак гипотенуза, а км - катет. поскольку, исходя из условия, катет км = 9/18 = 1/2 ак, то ∠кам = 30°.
т.к. по условию ак - биссектриса, то ∠сак =∠кам = 30°
рассмотрим δакс. по условию ∠аск = 90°; а∠сак = 30°, значит, ∠акс = 180° - 90° - 30° = 60°
искомый ∠акв - смежный с ∠акс, значит, ∠акв = 180° - ∠акс = 180° - 60° = 120°
ответ: 120°
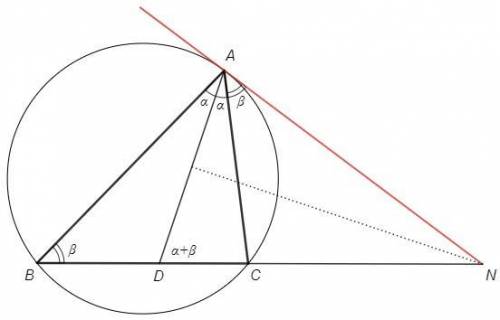
Точка N лежит на серединном перпендикуляре к AD, следовательно равноудалена от концов отрезка.
△AND - равнобедренный, DAN=ADN
DAN =A/2 +NAC
ADN =A/2 +B (внешний угол △BAD)
=> NAC =B =∪AC/2
Угол между прямой NA и хордой AC равен половине дуги, стягиваемой хордой, следовательно NA является касательной.
Докажем этот признак для острого угла NAC.
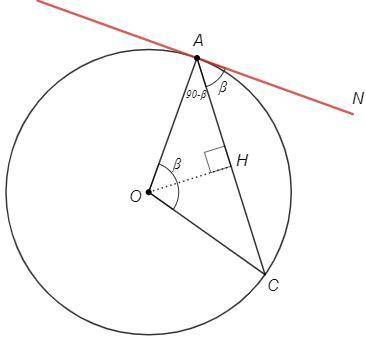
NAC =∪AC/2 =AOC/2 =AOH
△AOC - равнобедренный, OH - биссектриса и высота
OAH =90-AOH =90-NAC => OAN =OAH+NAC =90
Прямая NA перпендикулярна радиусу OA, следовательно является касательной.
Для тупого угла как для смежного с NAC:
180-NAC =(360-∪AC)/2 => NAC=∪AC/2, далее по доказанному.
Точка М - середина отрезка АN, a точка N - середина отрезка ВМ.
Следовательно
А = (2 * 1 - (-3); 2 * (-1) - 2; 2 * 2 - 4) = (5; -4; 0)
В = (2 * (-3) - 1; 2 * 2 - (-1); 2 * 4 - 2) = (-7; 5; 6)