См. Объяснение.
Объяснение:
1) При пересечении AB и CD образуются два равных треугольника:
ΔАОС = ΔDОB, так как две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника (первый признак равенства треугольников), а именно:
АО = ОВ - согласно условию;
DO = ОС - согласно условию;
∠АОС = ∠DОB - как углы вертикальные.
2) В равных треугольниках против равных углов лежат равные стороны:
АС и BD лежат против равных углов ∠АОС и ∠DОB, следовательно:
АС=BD, - что и требовалось доказать.
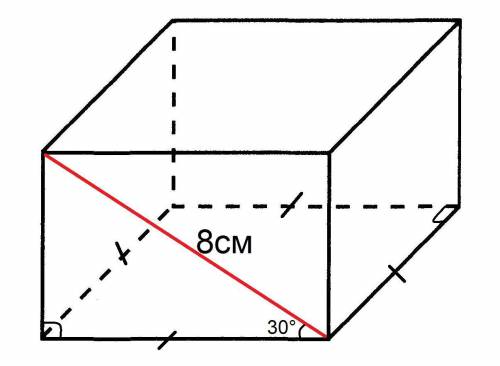
Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.