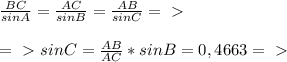
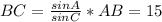
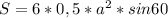 , где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что
, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 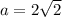 . Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=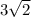 . Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
Прямоугольный треугольник МОС - равнобедренный, так как острый угол МСО равен 45° (дано). Следовательно, катеты равны и ОС=МО=10.
Заметим, что АО=ВО=СО=10.
В правильном треугольнике АВС СО=АО - это 2/3 его высоты, а ОН (расстояние от центра О до стороны ВС равно 1/3 его высоты (так как высота = медиана и точкой О делится в отношении 2:1, считая от вершины. Значит ОН=ОС:2=5. В прямоугольном треугольнике МОН, где гипотенуза МН - искомое расстояние, по Пифагору найдем МН=√(МО²+ОН²) или МН=√(100+25) = 5√5.
ответ: МН=5√5.