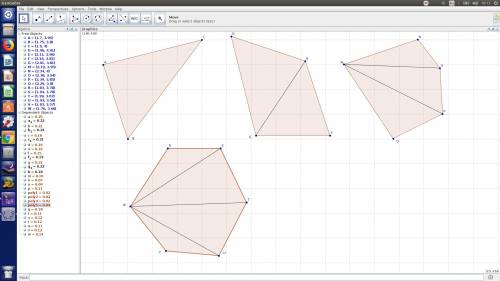
Решить! 1. дано (рис. 1): вершины двух равных перпендикуляров ав и cd длиной 12 соединены отрезком вс, который поделен пополам точкой f. из точки d проведен перпендикуляр de к ad, равный 8. fe=15. найти длину отрезка вс. 2. дано (рис. 2): из вершины с прямоугольника abcd (ab-cd a ad-bc=b) восстановлен перпендикуляр cs, равный (. определить угол dsb.
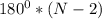
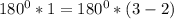
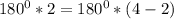
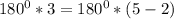
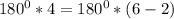
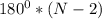 (строго доказываеться с метода математической индукции)
(строго доказываеться с метода математической индукции)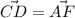
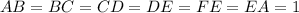
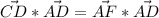 будем за опредилением через угол:
будем за опредилением через угол: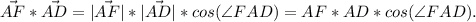
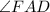 и длину стороны
и длину стороны  .
.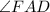 :
: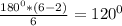
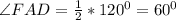
 :
: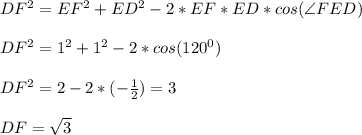
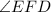
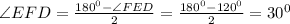
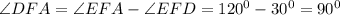
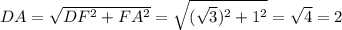
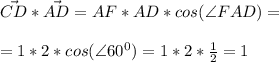
Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен см. Найдите стороны треугольника
Объяснение:
ΔАВС, ∠В=120°, О-центр описанной окружности. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к его сторонам.
Пусть ВН⊥АС, О∈ВН., ОВ=ОА=6√3 см.
По теореме синусов( отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности) :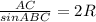 ,
, 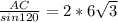 , АС=12√3*
, АС=12√3*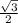 =18 (см).
=18 (см).
По свойству высоты равнобедренного треугольника ∠АВН=∠НВС=60°, АН=НС=9 см.
ΔАВН-прямоугольный , sin 60°=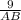 , АВ=6√3 см ⇒ВС=6√3 см.
, АВ=6√3 см ⇒ВС=6√3 см.