См. Объяснение
Объяснение:
∠В треугольника АВС равен ∠АСD треугольника ACD - согласно условию (отмечены одинаковыми дужками);
∠ВСА треугольника АВС равен ∠САD треугольника ACD - так как, согласно условию, ADCD является трапецией, поэтому AD║ BC, и угол
∠ВСА = ∠САD как углы внутренние накрест лежащие при параллельных прямых AD║ BC и секущей АС.
Согласно первому признаку подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Что и требовалось доказать.
ответ: Р=42см
Объяснение: проведём вторую диагональ ВД. Пусть точкой их пересечения будет точка О. Так как диагонали ромба, пересекаясь делятся пополам, образуют прямой угол и делят углы пополам, то АО=ОС=½×АС=10,5÷2=5,25см. Рассмотрим ∆АВО. В нём угол АОВ=90°(его образуют диагонали. Зная, что угол В=60°, то угол АВО= 60÷2=30°. В этом треугольнике АОВ, катет АО лежит напротив угла 30°, а значит равен половине гипотенузы АВ. АВ=5,25×2=10,5см. Теперь найдём периметр ромба, зная его сторону:
Р=10,5×4=42см; Р=42см
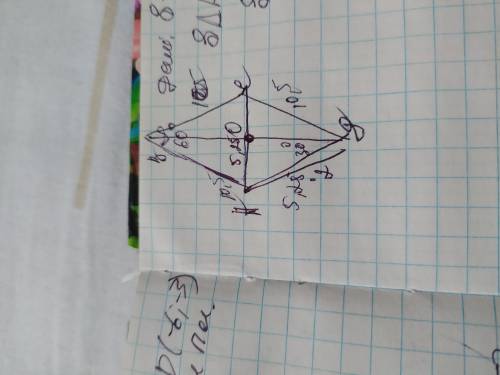
Нужно провести высоту. S сечения = 1/2высоты*сторону. Неизвестна только высота.
(Против угла в 30градусов) ((180-120)/2) нужно найти гипотенузу