исходя из этих данных можно решить только в случае, если исходный треугольник мре - равнобедренный, с равными сторонами мр и ре.тогда все легко.ра - является в данном случае и биссекриссой и высотой.и у нас 2 прямоугольных треугольника мра и аре, в которых ма=ае=в/2 (т.к. высота в равнобедренном треугольнике делит основание пополам).собствено дальше все решение основано на свойствах прямог. треугольника, а именно.мр - это гипотенуза мра, и равнамр = ма * синус (бетта/2)=в/2 *синус (бетта/2)а ра - это катет того же прямоуг треугольника, и он равен ра=ма/тангенс (бетта/2)=в/2 / тангенс (бетта/2)
но если треугольник мре - произвольный, то боюсь решить не получится, хотя мне кажется он все-таки равнобедренный.удачи
а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен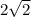 
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,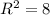 
, 
.
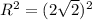
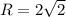в) (5; -7) - центр окружности, R²=16,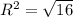 
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
в равнобедренном треугольнике основание равно 16 см, а биссектриса, проведенная к основанию, равна 18 см. найдите медиану, проведенную к боковой стороне