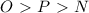- всё это конечно углы.
тут всё очевидно же
Объяснение:
Средняя линия треугольника и её свойства. Определение: средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. У средней линии есть два свойства : первое свойство: средняя линия треугольника параллельна основанию и второе свойство: средняя линия равна половине основания. Доказательство. Через середину E боковой стороны BC проведём прямую ED параллельно основанию AC. По теореме Фалеса другая боковая сторона тоже разделится пополам. Значит, D — середина стороны AB, то есть отрезок ED — это средняя линия. А по построению наш отрезок параллелен основанию, вот и доказана параллельность средней линии основанию. Теперь докажем второе свойство: через точку D проведём прямую DF, параллельную боковой стороне BC. По теореме Фалеса основание AC разделится пополам, то есть точка F — середина стороны AC, и FC равно половине основания. А многоугольник CEDF — это параллелограмм (по построению), его противоположные стороны равны, то есть отрезок DE равен половинке основания — отрезку FC. То есть средняя линия равна половине основания. ЧТД.
Прямой угол АОВ разделен углом ОС на два угла: угол АОС и угол СОВ, т.е. АОВ=АОС+СОВ.
Один из получившихся углов (пусть это будет АОС) на 12 градусов больше другого, т.е. АОС=СОВ+12 градусов.
Соответственно, АОВ=СОВ+СОВ+12 градусов.
По условию, АОВ=90 градусов.
90=СОВ+СОВ+12
90=2*СОВ+12
2*СОВ=90-12
2*СОВ=78
СОВ=78:2
СОВ=39 градусов - градусная мера меньшего из получившихся углов.
Тогда АОС=СОВ+12=39+12=51 градус - градусная мера большего из получившихся углов.
ответ: 39 градусов; 51 градус.