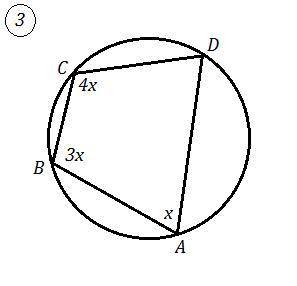
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна 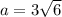 .
.
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть 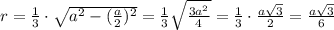 .
.
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна 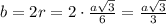 .
.
Периметр квадрата равен 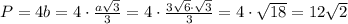 см.
см.
Расстояние от точки до плоскости равно длине перпендикулярного к ней отрезка.
Обозначим вершины ромба АВСD.
Точка L удалена от прямых, содержащих стороны ромба, на одинаковое расстояние. ⇒ наклонные, проведенные из L перпендикулярно к сторонам ромба, равны, и по т. о з-х перпендикулярах равны их проекции.
Эти проекции равны половине диаметра вписанной в ромб окружности, который равен высоте ВН ромба. Центр окружности лежит на пересечении диагоналей ромба.
ВН=АВ•sin 45°=(a√2)/2=a/√2.
Радиус ОK=а/2√2.
По т.Пифагора из ∆ LOK катет LO=√(LK²-OK²)
LO=√(b²- a²/8) Домножив в подкоренном выражении числитель и знаменатель на 2, получим LO=√[2•(8b²-a²):16]=[√2•(8b²-a²)]:4

МО²=КО²+МК²
МК²=МО²-КО²
МК=√17²-15²=8см
2)диагональ образует прямоугольный треугольник , значит диагональ²=8²+15²
диагональ= 17см