Площадь трапеции равна 900√3 м²
Объяснение:
Дано:
ABCD - трапеция
АС - диагональ трапеции
AB = CD - боковые стороны
АС ⊥ CD
AD = 40√3 м - большее основание
∠A = ∠D = 60°
Найти:
S - площадь трапеции
Рассмотрим прямоугольный треугольник ACD, гипотенуза которого AD = 40√3 м и ∠D = 60°.
Катеты АС и CD этого треугольника равны
АC = AD · sin 60° = 40√3 · 0.5√3 = 60 (м)
CD = AD · cos 60° = 40√3 · 0.5 = 20√3 (м)
Поскольку трапеция равнобедренная, то
АВ = CD = 20√3 м.
Из вершины С прямого угла треугольника ACD опустим на гипотенузу AD высоту CK, которая одновременно является и высотой трапеции
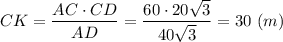
В треугольнике ACD
∠CAD = 90° - ∠D = 90° - 60° = 30°
Основания трапеции ВС ║ АD
∠ACB = ∠CAD = 30° (внутренние накрест лежащие углы при ВС ║ АD и секущей АС).
Рассмотрим ΔАВС.
∠ВАС = ∠BАD - ∠CAD = 60° - 30° = 30°
Поскольку в ΔАВС углы ∠ВАС = ∠ACB = 30°, то ΔАВС - равнобедренный, то есть ВС = АВ = 20√3 м.
Площадь трапеции равна произведению полусуммы оснований на высоту.
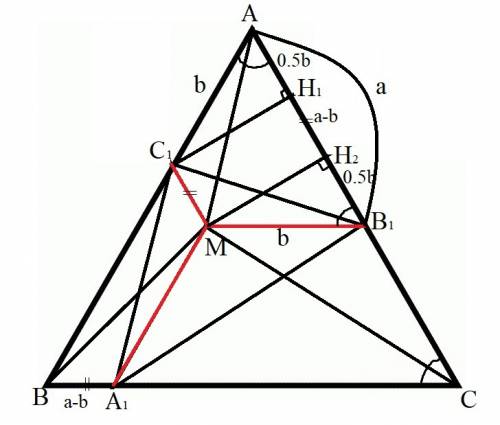
Пусть MA₁║AB, MB₁║BC, MC₁║AC.
Рассмотрим фигуру AB₁MC₁. Т. к. MC₁║AC ⇒ MC₁║AB₁, AC₁∦MB₁ ⇒ AB₁MC₁ - трапеция. Т. к. ∠A = ∠C, ∠C = ∠AB₁M как соответственные ⇒ ∠A = ∠AB₁M ⇒ AC₁ = MB₁, т. е. трапеция равнобедренная ⇒ B₁C₁ = AM как диагонали равнобедренной трапеции.
Аналогично рассуждая, C₁A₁ = BM, A₁B₁ = CM, что и требовалось доказать.
Пусть C₁H₁⊥AB₁, MH₂⊥AB₁. Тогда MC₁H₁H₂ - прямоугольник ⇒ H₁H₂ = C₁M. Т. к. A₁BC₁M - равнобедренная трапеция, A₁B = C₁M ⇒ A₁B = H₁H₂.
В прямоугольном треугольнике AH₁C₁ AH₁ = AC₁ * cos A = b * cos 60° = 0.5b. Аналогично B₁H₂ = 0.5b. Тогда H₁H₂ = AB₁ - AH₁ - H₂B₁ = a - 0.5b - 0.5b = a - b ⇒ A₁B = a - b.
ответ: a - b
ответ: 20.
0_0