Объяснение:
7. В треугольниках △ABD и △CBD DC=AD, AB=BC по условию, BD - общая сторона, значит △ABD=△CBD по 3му признаку. => <ABD=<CBD
8. В треугольниках △ABC и △ADC <BAC=<CAD, <BCA=<DCA по условию, АС - общая сторона, значит △ABC=△ADC по 2му признаку. => AD=AB=9cм, CD=BC=3см, АС (общая) =10см.
Р(ADC)=AD+CD+AC=9+3+10=22см
9. <OCN=<ONC => △CON - равнобедренный и тогда OC=ON.
Тогда в треугольниках △DCO и △DNO СD=DN по условию, OC=ON по доказанному выше, OD - общая сторона => △DCO=△DNO по 3му признаку.
Объяснение:
109)1)
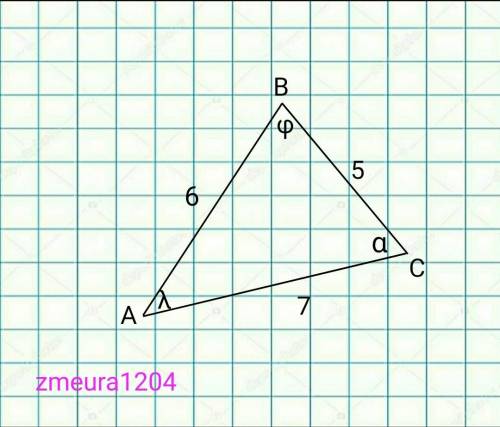
cos<λ=(AB²+AC²-BC²)/(2*AB*AC)=
=(6²+7²-5²)/(2*6*7)=(36+49-25)/84=
=60/84=5/7
cos<φ=(AB²+BC²-AC²)/(2*AB*BC)=
=(6²+5²-7²)/(2*6*5)=(36+25-49)/60=
=12/60=1/5
cos<α=(ВС²+СА²-АВ²)/(2*ВС*СА)=
=(5²+7²-6²)/(2*5*7)=(25+49-36)/70=
=38/70=19/35
ответ: cos<α=19/35; cos<λ=5/7; cos<φ=1/5
109)2)
Дано:
Треугольник
а=5м сторона
b=6м сторона
sin<α=0,6, где <α- угол между а;b
c=?
Решение
Тригонометрическое тождество
sin²α+cos²α=1
cos<α=√(1-sin²α)=√(1-0,6²)=√(1-0,36)=
=√0,64=0,8.
Теорема косинусов
c=√(a²+b²-2*a*b*cos<α)=√(5²+6²-2*5*6*0,8)=√(25+36-48)=√13м третья сторона треугольника
ответ: √13 м
(х²-х)+(у²-у)=0
Прибавим ко обеим частям неравенства два раза по 1/4
(х²-х+(1/4)) +(у²-у+(1/4))=1/4+1/4
(х-(1/2))²+(у-(1/2))²=(1/√2)²
Это и есть уравнение окружности с центром в точке (1/2; 1/2) радиусом 1/√2