ответ: Р=38см
Объяснение: обозначим вершины треугольника А В С а точки касания Д К М. Причём Д лежит на АВ; К- на ВС; М- на АС. Стороны треугольника являются касательными к вписанной окружности, и отрезки касательных, соединяясь в одной вершине равны, от точки касания до вершины треугольника. Поэтому ВД=ВК=7см; АД=АМ=5см; СК=СМ=5см. Из этого следует что АМ=СМ=5см. Теперь сложим эти отрезки сторон:
АВ=ВС=5+7=12см; АС=7+7=14см. Зная все стороны треугольника найдём его периметр: Р=12+12+14=24+14=38см
Объяснение:
понял
Рассмотрим основание ABC.
Наименьшая высота опушена к наибольшей стороне
наибольшая высота - к наименьшей стороне
средняя высота AH - к средней стороне BC=14
Следует из формулы площади треугольника:
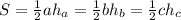
Площадь ABC по формуле Герона

p =(13+14+15)/2 =21
S =√(21*8*7*6) =84
S =1/2 BC*AH => AH =2*84/14 =12
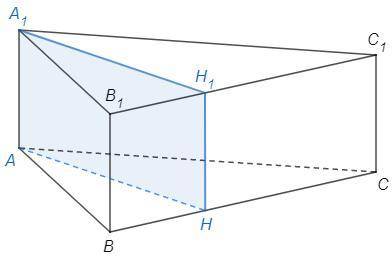
AA1H1H - данное сечение
(AH и ребра BB1 и CC1 скрещиваются, то есть не лежат в одной плоскости)
Боковые ребра прямой призмы перпендикулярны основанию (=> высота равна боковому ребру)
Сечение через боковое ребро прямой призмы - прямоугольник.
S(AA1H1H) =AA1*AH => AA1 =60/12 =5
V =S(ABC)*AA1 =84*5 =420 (см^3)
длина дуги =10п,градусная мера дуги 150 градусов
значит дуге =1п отвечает угол 15 градусов
тогда длина круга, которое отвечает угол 360 градусов=15градусов*24
будет 24п
длина окружности равна 2п*радиус=24 п
значит радиус равен 12
площадь круга равна п*радиус*радиус=12*12*п=144 п