192см²
Объяснение:
Дано
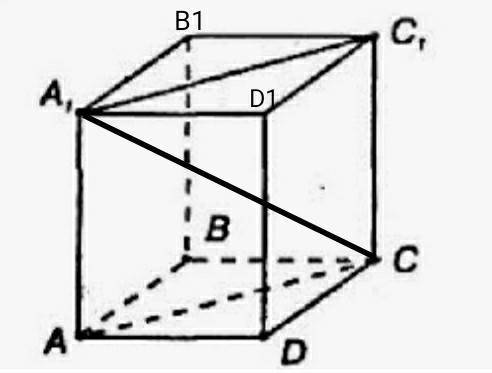
ABCDA1B1C1D1 - параллелепипед
AD=4см
DC=12cм
А1С=13 см.
Sпол=?
Решение.
∆ADC- прямоугольный
По теореме Пифагора найдем гипотенузу
АС²=АD²+DC²=4²+12²=16+144=160 см
AC=√160 см
∆АА1С- прямоугольный.
По теореме Пифагора найдем катет
АА1=А1С²-АС²=13²-(√160)²=169-160=9
АА1=√9=3см.
Sбок=Рaвсd*AA1
Paвсd=2*4+2*12=8+24=32 см периметр прямоугольника АВСD.
Sбок=32*3=96см². площадь боковой поверхности параллелепипеда
Sосн=АD*DC=4*12=48 см² площадь прямоугольника ABCD.
Sпол=2*Sосн+Sбок=2*48+96=192 см² площадь полной поверхности параллелепипеда.
Четырехугольник АВСD - кавдрат, то есть прямоугольник. Что и требовалось доказать.
Объяснение:
Вершины четырехугольника А(3,-1), В(2,3), С(-2,2), D(-1,-2).
1. Найдем длины сторон четырехугольника.
|AB| = √((Xb-Xa) ²+(Yb-Ya) ²) =
√((2-3)²+(3-(-1))²) = √(1+16) =√17.
|CD| = √((Xd-Xc) ²+(Yd-Yc) ²) =
√((-1-(-2))²+(-2-2)²) = √(1+16) =√17.
|BC| = √((Xc-Xb) ²+(Yc-Yb) ²) =
√((-2-2)²+(2-3))²) = √(16+1) =√17.
|AD| = √((Xd-Xa) ²+(Yd-Ya) ²) =
√((-1-3)²+(-2-(-1))²) = √(16+1) =√17.
Так как ВСЕ стороны четырехугольника равны, то этот четырехугольник является или ромбом, или квадратом.
Найдем угол между соседними сторонами:
CosA = (Xab*Xad + Yab*Yad)/(|AB|*|AD|) =
(-1*-4 + 4*-1)/(|AB|*|AD|) = 0/17 = 0.
Так как угол А прямой (<A = arccos0 = 90°), следовательно, четырехугольник является квадратом, то есть ПРЯМОУГОЛЬНИКОМ. Что и требовалось доказать.
Известно, что если в четыриугольник вписана окружность, то сума его противоположных сторон равна, отсюда сума основ трапецыи равна 30/2=15см.
А средняя линия равна полсуме основ, и она равна 15/2=7,5см.
ответ:7,5см.