Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
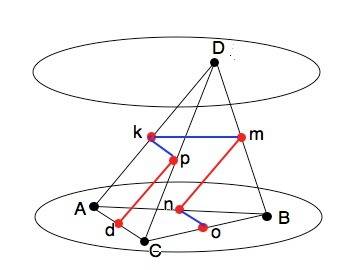
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
свойство прямоугольного треугольника
Высота ,опущенная на гипотенузу делит её на отрезки , пропорциональные катетам.
Стороны прямоугольника a,b - это катеты. Диагональ ВД -гипотенуза.
тогда
a : b =1 : 3 ; b=3a
BD^2=a^2+b^2 =a^2+(3a)^2=10a^2
6^2=10a^2
a=6/√10
b=3*a=3*6/√10=18/√10
расстояние от точки пересечения диагоналей до большей стороны - это
половина меньшей стороны
a/2=6/√10 /2=3/√10 или тоже самое 3√10/10 или 0.3√10
ОТВЕТ
** на выбор