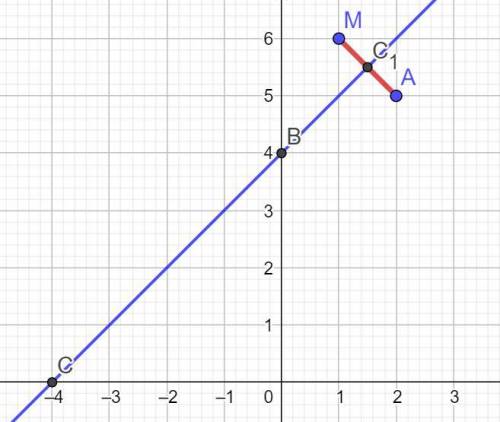
Геометрическое место точек, равно удалённых от точек А и В - это срединный перпендикуляр к отрезку АМ.
Пусть точка пересечения этого перпендикуляра с осью Оу (ось ординат) - это точка В(0; у).
Векторы: АВ = (0-2=-2; (у-5)) = (-2; (у-5)),
МВ = (0-1=-1; (у-6)) = (-1; (у-6)).
Расстояния: АВ² = 4 + у² - 10у + 25 = у² - 10у + 29.
МВ² = 1 + у² - 12у + 36 = у² - 12у + 37.
Приравняем: у² - 10у + 29 = у² - 12у + 37.
Отсюда 2у = 8, у = 8/2 = 4.
ответ: точка В(0; 4).
Высота треугольника - перпендикуляр, опущенный из вершины угла треугольника на прямую, содержащая противоположную сторону.
Если ты в седьмом классе, то вот основные свойства, которые проходят в этом классе :
Всё высоты пересекаются в одной точке - ортоцентре.
В остроугольном треугольнике все высоты лежат внутри этого треугольника.
В тупоугольном треугольнике две высоты (которые проведены из вершин острых углов) лежат вне треугольника, а высота, проведённая из вершины тупого угла, лежит внутри.
В прямоугольном треугольнике две его высоты совпадают с его катетами. Также, высота, проведённая к гипотенузе, делит его на три треугольника с теми же острыми углами.
В равнобедренного треугольнике высота, проведённая к основанию - это биссектриса и
медиана.
В равностороннем треугольнике все высоты равны, а также совпадают со всеми медианами и биссектрисами.
Для восьмого класса :
Всё высоты треугольника обратно пропорциональны его сторонам (это значит, чем больше высота, тем меньше сторона, к которой проведена эта высота. Также верно и обратное утверждение.)
В прямоугольном треугольнике высота, проведённая к гипотенузе - среднее геометрической между проекциями катетов на эту гипотенузу.
Центром описанной вокруг треугольника окружности является точка пересечения срединных перпендикуляров. Центром вписанной в треугольник окружности является точка пересечения биссектрис.
В равностороннем треугольнике эти точки совпадают. А так как высоты ( срединные перпендикуляры) такого треугольника в то же время и его биссектрисы и медианы, а медианы треугольника точкой пересечения делятся в отошении 2:1, то и радиусы данных окружностей имеют такое же отошение.