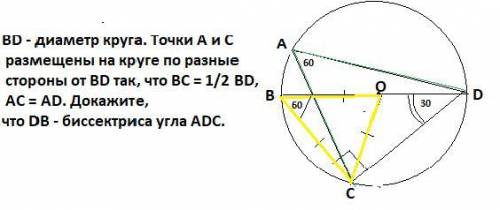
BD - диаметр круга. Точки А и C размещены на круге по разные стороны от BD так, что BC = 1/2 BD, AC = AD. Докажите, что DB - биссектриса ∠ADC.
Объяснение:
1) Т.к. BC= 1/2*BD=ВО ,и ВО=ОС как радиусы , то ΔВОС -равносторонний ⇒∠СВD=180°:3=60°.
2) На дугу СD опираются два вписанных угла ⇒ по свойству вписанных углов ∠CBD=∠CAD=60°
2)Точки C размещена на окружности ⇒∠ВСD=90° , тк опирается на диаметр BD. Значит ∠ВDС=90°-60°=30°.
3) Т.к. AC=AD ,то ΔCAD-равнобедренный ⇒∠АСD=∠ADС=(180°-60°):2=60°. Поэтому на частичку угла ∠ADB=60°-30°=30°
4) Получили ∠ADB=30°( п 3)
∠ВDС=30°( п 2)⇒ DB - биссектриса ∠ADC.
` ` — Здравствуйте, Levva007! ` `
• Объяснение:
— | Прежде чем нам решить данную задачу, сначала нужно отметить в ней главные слова: | —
• Первый участок имеет форму прямоугольника со сторонами 360 м и 90 м, второй участок имеет форму квадрата.
— | Отметили. Теперь, когда мы знаем главные слова в данной задаче, мы можем начать её решать. | —
• Решение:
• 1. Сначала, мы с вами должны узнать площадь прямоугольника. Это записывается так:
1)360 ˣ 90 = 32 400 ( м² ) – площадь прямоугольника.
• 2. Теперь, мы можем узнать периметр прямоугольника. Это записывается так:
2)360 ˣ 2 + 90 ˣ 2 = 900 ( м ) – периметр прямоугольника
• 3. Теперь, мы узнаём сторону квадрата. Это записывается так:
3)900 : 4 = 225 ( м ) – сторона квадрата
• 4. А теперь, мы можем узнать площадь квадрата, и потом в пятом действии записать и сравнить, чья площадь больше – квадрата или прямоугольника. Но смотря, какая у вас программа : если у вас программа Л.Г. Петерсона, то записывать нужно, но, а если у вас программа Рудницкой или Моро и др., то не нужно. Это записывается так:
4)225 ˣ 225 = 50 625 ( м² )
• 5. А вот когда мы узнали площадь квадрата и прямоугольника, то мы можем сравнить, чья площадь больше. Это записывается так:
5)50 625 > 32 400
• или...
5)32 400 < 50 625
• 6. А вот на сколько площадь квадрата больше площади прямоугольника мы не знаем. Но мы можем решить! Для этого нам нужно:
6)50 625 – 32 400 = 18 225 ( м )
— | Мы узнали то, что площадь квадрата больше площади прямоугольника. И на сколько. Мы можем записать ответы. ответы, потому что у нас в данной задаче два во ответ: Площадь участка квадратной формы больше площади участка прямоугольной формы; на 18 225 м площадь участка квадратной формы больше площади участка прямоугольной формы.
` ` — С уважением, EvaTheQueen! ` `
CH-высота⇒<HCD=30⇒DH=3cм противугла в 30гр
CH=AB=6*cos30=6*√3/2=3√3см
AD=BC+DH
Чтобы можно было вписать окружность,нужно чтобы
AB+CD=BC+AD
3√3+6=2BC+3
2BC=3√3+3
BC=(3√3+3)/2