1) из прямоугольного треугольника выразим длину и ширину через диагональ и известный угол и подставим вформулу периметра
(d sin 39 + d cos 39)=70
d sqrt(2) (sin 39 cos 45 + cos 39 sin 45)=70
d sqrt(2) sin 84 = 70
d=70/( sqrt(2) sin 84 )
теперь нетрудно найти стороны
AB= 31.32
BC = 38.68
2) Построим ромб и опустим высоту OC на сторону AB.
Угол BCA=BAC = 70 Угол OCA=20 - из суммы углов треугольника.
Теперь из прямоугольного треугольника OCA найдем высоту ромба
OC = AC sin 20
OC= 4.79
3) Рисунок - половина решения.
Для двух прямоугольных треугольников распишем соотношение сторон через гипотенузы и углы
AC= AB cos a
AC = AD cos (a-b)
BC= AB sin a
CD = AD sin (a-b)
выразим AD= AB cos a/ cos(a-b)
BD=BC-CD
BD= AB sin a- AB sin(a-b)/cos (a-b) cos a= AB (sin a - tg (a-b) cos a)
или BD=c( sin a - tg(a-b) cos a)
15 см
Объяснение:
Периметр квадрата равен 20
S=4a=20 см
a= 5 см
Сторона квадрата равна 5 см
Если провести диагональ в квадрате, и найти среднюю линию (которая также радиус) то решение пойдёт быстрее
то есть радиус равен половине стороны квадрата- то есть 2.5 см
внутри у правильного шестиугольника все стороны от центра равны 2.5 см
если проведём от центра до углов прямые, то получим равнобедренные треугольники
стороны при основании равны
в центре угол равен 360/6=60
значит мы получаем правильные треугольники и сторона шестиугольника равен 2.5см
P=6*2,5=15 см
(Сделай лучшим)
(Рисунок к задаче 8)
6) Дано:
Трикутник ABC
Кут BAZ = 150° (точка z - за межею завершенного відрізка CA)
Кут ACB = 110°
x - ?
Розв'язання:
Кут CAB, за властивістю суміжних кутів (сума суміжних кутів дорівнює 180°) дорівнює 180°-150°=30°. Сума всіх кутів трикутника дорівнює 180°. 180-110-30=40° (кут ABC). Знову використовуємо властивість суміжних кутів. 180-40=140° = x
Відповідь: x = 140°
7) Дано:
Трикутник ABC
Вертикальний кут до кута CAB = 62°
Кут ABC = 80°
x - ?
Розв'язання:
Кут, що даний і дорівнює 62° вертикальний до кута CAB, а оскільки вертикальні кути дорівнюють один одному - кут CAB дорівнює 62°. Сума всіх кутів трикутника дорівнює 180°. Кут BCA дорівнює 180°-80°-62°=38°. Оскільки вертикальні кути дорівнюють один одному то кут вертикальний до кута BCA дорівнює йому. Їх сума - 76°. Коло - 360°. x = (360-76)/2=142°
Відповідь: x = 142°
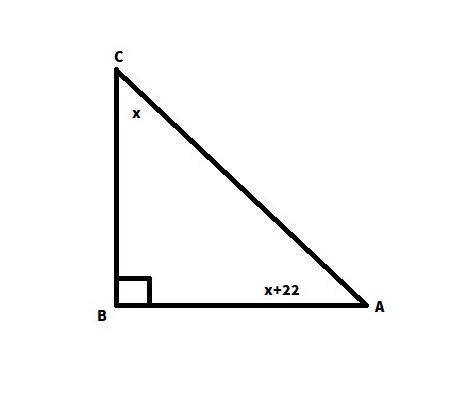
8) Дано:
Трикутник ABC (Кут B = 90°)
Кут A - Кут C = 22°
Кут C - ?
Розв'язання:
Сума всіх кутів трикутника дорівнює 180°. Сума двох гострих кутів прямокутного трикутника дорівнює 90°.
90° = x + x +22°.
68°=2x
34°=x=Кут С
Відповідь: Кут С (менший з гострих кутів трикутника) дорівнює 34°
Т-cos: a^2=b^2+c^2-2bc*cos угла
Т-sin:a/sina=b/sinb=R то есть радиусу описанной окружности