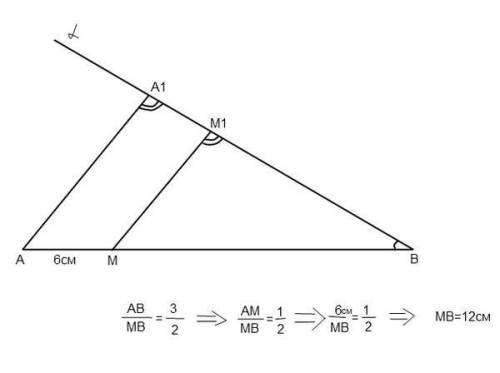
В треугольнике угол A=30° угол C=45° а высота BD= 4 см.
Найдите стороны треугольника.
----------------------
Высота ВД противолежит углу, равному 30º. ⇒ BD равна половине гипотенузы ∆ АВД.
Гипотенуза АВ=4*2=8 см.
АD найдем по т.Пифагора:
АD²=АВ²-ВD²
АD=√(64-16)=√48
АD=4√3 см
В прямоугольном ∆ ВDС острый угол ВСD=45º, ⇒ угол СВD=45º,
∆ СВD - равнобедренный, СD=ВD=4 см
По т.Пифагора ВС=4√2 см ( проверьте)
Тогда АС=АD+DС=4√3+4=4(√3+1)
Стороны равны
АВ=8,
ВС=4√2
AC =4(√3+1)
-----------
Если Вы уже изучали тригонометрические функции, то можно использовать их значение для заданных углов.
АВ=ВD:sin30º=4:0,5=8 см
BC=BD:sin45º=4:(√2)/2=4√2 см
АС=АD+DС=4√3+4=4(√3+1) см
Т.к. М-середина отрезка АВ, то АМ=МВ. Т.к. основания трапеции параллельные , т.е. ВС//AD, то и К-середина отрезка СD, и => CK=KD. Получаем, что МК- средняя линяя трапеции ABCD. МК=(AD+BC)/2=(10+4)/2=7см
Объяснение:
2. МN - средняя линия треугольника которая, как известно, параллельна его основанию. А основание треугольника в данном случае является и стороной прямоугольника. Противоположные стороны которого (как тоже должно быть известно) параллельны. Стало быть, имеем MN || ВC и ВС || AD => MN || AD=4
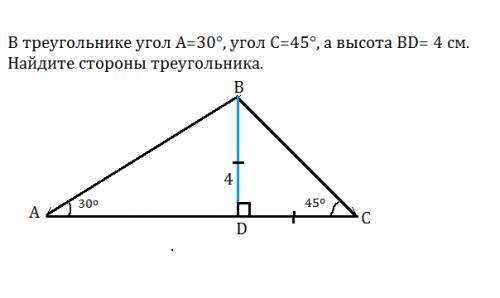
3. А1, М1 и В лежат на одной прямой т. к. эти точки являются точками пересечения с Альфа прямых АВ, АА1, ММ1.
Треугольники АА1В и ММ1В подобны по первому признаку подобия треугольников. (Признак 1 Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника. ) ( угол с вершиной в т. В у них общий, а углы АА1В и ММ1В равны, т. к. АА1 параллельна ММ1)
А так как треугольники подобны то и стороны у них подобны.
Если АА1:ММ1=3:2, то АВ: МВ=3:2 следовательно АМ: МВ=1:2 если АМ=6см, то 6:МВ=1:2 из этой пропорции находим МВ. Получаем МВ=12см