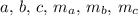 - длины сторон и медиан треугольника ABC,
- длины сторон и медиан треугольника ABC, 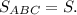 Воспользовавшись формулу
Воспользовавшись формулу 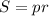 и то, что
и то, что 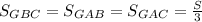 , получаем, что нужно доказать неравенство.
, получаем, что нужно доказать неравенство.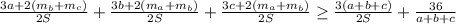
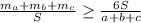
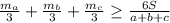
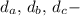 расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что
расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что 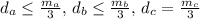 Также имеем
Также имеем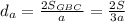 . Аналогично,
. Аналогично, 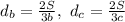
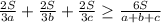 , которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел:
, которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел: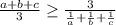
1) Периметр треугольника равен P=a+b+c
Так как a=b=a, а c=a/2 то,
P=a+a+a/2
40=(4a+a)/2
80=5a
a=16
c=16/2=8
И того: a=b=16; c=8
2)(см. рисунок в приложениях)
Медиана делит этот треугольник на 2 равновеликих(равных)
Тоесть ABD=CAD
если точки m и k являються серединами сторон разных(но равных) треугольников, то соответственно BKD=BMD
3) Нарисовали ресунок
ABC - треугольник BH - высота
Они равны так как:
1) Сторона BH - общяя
2) угол BAH = углу BCH (как углы равнобедренного треугольника)
3) Угол AHB=AHC как углы при высоте(прямые)
4) Сторона AB= строное BC( как стороны равнобедренного треугольника)
Значит, треугольники равны