Объяснение:
1.Градусная мера дуги, на которую опирается центральный угол, равна 80 °. Определить градусную меру этого угл
а) 120° б) 80° в) 40°г) 50°
Центральный угол равен градусной мере дуги, на которую опирается. Поэтому ответ б) 80 градусов
2.Градусная мера центрального угла равна 120 °. Определить градусную меру дуги, на которую он опирается.
Из аналогичных соображений ответ г) 120 градусов.
а) 160° б) 90° в) 60°г) 120°
3.Градусная мера вписанного угла равна 140 °. Определить градусную меру дуги, на которую он опирается.
Вписанный угол равен половине градусной меры дуги на которую опирается. Поэтому градусная мера дуги равна 140*2 = 280 градусов. ответ в) 280 градусов.
а) 100° б) 70° в) 280°г) 140°
4.Градусная мера дуги, на которую опирается вписанный угол, равна 90°.Определить градусную меру этого вписанного угла.
Из аналогичных соображений, вписанный угол равен половине градусной меры дуги, на которую опирается. Следовательно, угол равен 90/2 = 45 градусов. ответ б) 45 градусов.
а) 100° б) 45° в) 180°г) 90°
5.Определить градусную меру угла, вписанного в окружность, если соответствующий ему центральный угол равен 126 ° .
Центральный угол равен градусной мере дуги, на которую опирается, а вписанный угол половине дуги. Следовательно, вписанный угол равен половине центрального угла, опирающегося на ту же дугу. ответ а) 63 градуса.
а) 63° б) 252° в) 180°г) 126°
6.Определить градусную меру центрального угла окружности, если градусная мера соответствующего ему вписанного угла равна 40 ° .
Из аналогичных рассуждений, центральный угол в 2 раза больше вписанного угла, опирающегося на ту же дугу. ответ г) 80 градусов.
а) 40° б) 20° в) 140°г) 80°
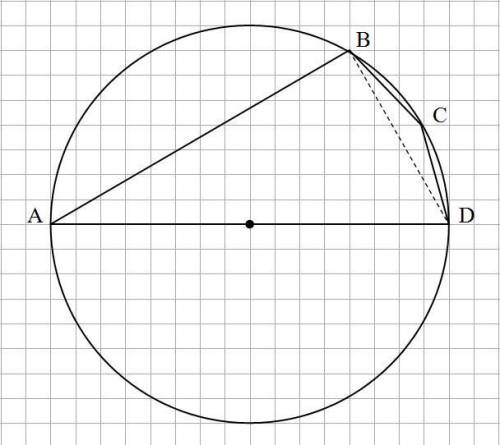
См. рис.
Так как AD - диаметр окружности, то угол ∠ABD = 90°
Следовательно, оставшийся угол прямоугольного
треугольника ΔABD: ∠BAD = 90 - 65 = 25°
Так как угол ∠BAD - вписанный, то величина дуги, на которую он опирается:
∪BCD = 2 · ∠BAD = 50°
Искомый угол ∠С = ∠BCD опирается на оставшуюся дугу
окружности:
∪BAD = 360 - ∪BCD = 360 - 50 = 310°
И величина угла ∠С = 310 : 2 = 155°
Причем, величина угла ∠С не зависит от местоположения точки С на дуге ∪BCD, так как в любом случае этот угол опирается на дугу ∪BAD, равную 310°
с боковыми ребрами = 10,
основание высоты ( = 8 ) которой -- точка (О) пересечения медиан Δ АВС
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины))
получили прямоугольный треугольник с гипотенузой 10,
катетом 8 и второй катет (АО) = (2/3) искомой медианы
по т.Пифагора АО = 6
медиана = (6 / 2) * 3 = 9
2) задача -- обратная 1)