Площадь треугольника равна половине произведения высоты на сторону, к которой проведена.
S=a•h:2
• Если высоты двух треугольников равны, то их площади относятся как основания.
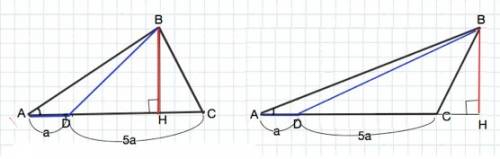
Высота ∆ ADC и ∆ ABC общая.
Подробно.
S(ABD):S(ABC)=AD:AC
Точка D по условию делит АС в отношении 1:5.
Примем AD=a, тогда DC=5a.
AC=а+5а=6a
S(ABD):A(ABC)=1/6
S(ABC)=36
S(ABD)=36:6=6 см²
-----------
Площадь треугольника можно найти и по формуле
S=a•b•sinα:2, где a и b стороны треугольника, α - угол между ними.
Угол А общий для ∆ABD и ∆ABC, поэтому
S (ABD):S (ABC)=AB•AD:AB•AC, т.е. получается то же отношение AD:AC, равное для данного треугольника 1/6.
Биссектриса ЕК делит СДЕ на два треугольника СКЕ и ЕКД. Треугольник СКЕ оказывается равнобедренным!
(т.к. половина угла Е это 38 градусов). Т.е. СК=КЕ.
В треугольнике КЕД угол Д равен 66 градусов, ДЕК=38 градусов, ДКЕ=76 градусов. В этом треугольнике большему углу соответствует большая противолежащая сторона. Т.е.КЕ (лежит противугла 66 град) больше , чем КД (лежит против угла 38 град.). А так как СК=КЕ, то СК больше, чем КД.
Что и требовалось доказать.