
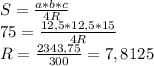
<A=67,5°
<D=67,5
<B=112,5°
<C=112,5°
Объяснение:
Дано
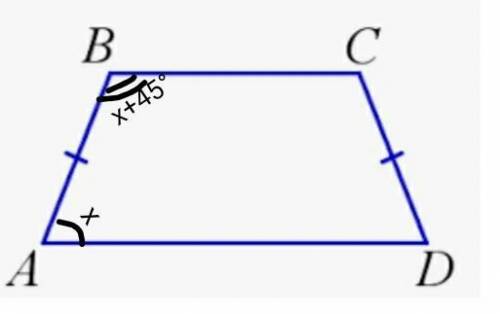
АВСD- равнобокая трапеция
АВ=CD
<A=?
<B=? на 45°больше >А
Найти <А; <В; <С;<D
Сумма углов прилежащих к боковой стороне трапеции равна 180°.
<А+<В=180°.
Пусть градусная мера угла <А будет х°, тогда градусная мера угла <В будет (х+45°).
Составляем уравнение
х+х+45=180
2х=180-45
2х=135
х=135/2
х=67,5° градусная мера угла <А
Градусная мера угла <В (х+45), подставляем значение х
67,5+45=112,5°
По свойствам равнобокой трапеции
<А=<D;
<B=<C
Можно провести биссектрису угла, тогда угол, лежащий против стороны в 30 гр = 1/2 гипотенузы т.е 3/2=1.5(одна часть); 6/2=3(вторая часть), 1.5+3=4,5 см