Основание равнобедренного треугольника относится к его высоте, проведенной к основанию, как 3 : 2, боковая сторона треугольника равна 20 см. Найдите периметр треугольника (в см).
Объяснение:
Δ АВС, АВ=ВС=20 см, ВН-высота, АС:ВН=3:2 . Р-?
Высота в равнобедренном треугольнике является медианой, значит АН=НС.
Пусть АН=х см, АС=2х см ⇒ (2АН) :ВН=3:2 , ( 2х):ВН=3:2 ,ВН=(4х)/3.
ΔАВН-прямоугольный, по т. Пифагора АВ²=АН²+ВН² ,
400=х²+(16х²)/9 , (25х²)/9=400 , х²=144 , х=12.
АС=2*12=24 (см)
Р=20+20+24=64(см)
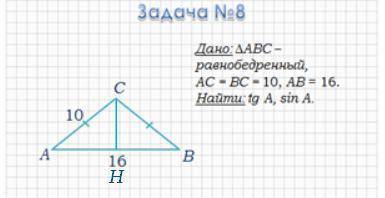
Задача: Дан ΔABC — равнобедренный, AC = BC = 10, AB = 16. Найти tg A, sin A.
Проведем высоту CH в ΔABC к стороне AB. Образуется два равных треугольника, т.к. ΔABC равнобедренный. AH = HB = 16/2 = 8.
Р-м ΔACH:
∠AHC = 90°, т.к CH — перпендикуляр к AH (AH∈AB) ⇒ ΔACH — прямоугольный.
Синус угла равен отношению противолежащего катета к гипотенузе.
Найдем катет CH за т. Пифагора:
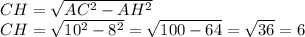
Тогда синус ∠A будет равен:
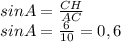
Тангенс угла равен отношению противолежащего катета к прилежащему:
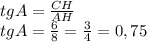
ответ: tg A = 0,75; sin A = 0,6.
Найти: АК-?
Построение: Так как в условии сказано об удалении точек от ребра двугранного угла, то прямые АС и ВС перпендикулярны к прямой z, содержащей ребро двугранного угла. Удаление точки от другой грани, говорит о том, что ВН перпендикулярно плоскости α и в частности прямой АС, а АК перпендикулярно плоскости β и в частности прямой ВС. Можно спроецировать весь этот рисунок на плоскость, перпендикулярную плоскостям α и β.
Решение: Имеется два треугольника ВСН и АСК с общим углом С. Рассмотрим синус (отношение противолежащего катета к гипотенузе) угла С для двух этих треугольников:
Левые части этих соотношенйи равны, так как речь идет об одном и том же углы, значит равны и их правые части:
Три отрезка из четырех даны по условию, длину четвертого нужно найти:
Уточнение: в условии не сказано какая именно из двух точек (удаленная от ребра на 4 см или на 10 см) удалена от второй грани на 5,5 см, но если предположить, что АС=10 см, ВС=4 см, то
ответ: 2,2 см