Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны. ⇒ а║b
Действительно: соответственные, внутренние и прочие углы при пересечении прямыми а и b прямой р равны.
Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
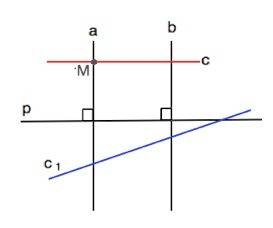
Пусть прямая с пересекает прямую а в точке М.
Допустим, что с не пересекает b. Тогда через точку М проходят две прямые, которые параллельны прямой b, что противоречит аксиоме
( В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой).
Заметим, что прямая с может быть параллельной прямой р или пересекать её ( на рисунке это с1).
Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны. ⇒ а║b
Действительно: соответственные, внутренние и прочие углы при пересечении прямыми а и b прямой р равны.
Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Пусть прямая с пересекает прямую а в точке М.
Допустим, что с не пересекает b. Тогда через точку М проходят две прямые, которые параллельны прямой b, что противоречит аксиоме
( В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой).
Заметим, что прямая с может быть параллельной прямой р или пересекать её ( на рисунке это с1).

я долго искала объяснение без тригонометрических преобразований (которые проходят уже в 10 классе)))
первая идея -- теорема косинусов, но нужен угол между радиусами...
первая часть решения -- понять как связаны углы в рассматриваемых треугольниках
углы АОВ и DOC --центральные
соответствующие им вписанные углы связаны в треугольник ВСК и их сумма равна внешнему углу, не смежному с ними, равна 60 градусов)))
значит, можно сделать вывод про сумму этих центральных углов --
она = 120 градусов
но эти углы из разных треугольников)))
а дальше тема Поворот (одна из заключительных тем геометрии 9 класса)))
если два треугольника с известными (данными) сторонами расположить рядом, то получится треугольник с углом 120 градусов и сторонами=радиусами
и треугольник с данными сторонами и с углом тоже 120 градусов -- т.к. это получится вписанный угол, опирающийся на дугу 360-120 = 240 градусов)))
и теперь по теореме косинусов радиус найти можно без сложных тригонометрических преобразований)))
значение косинуса угла в 120 градусов в 9 классе уже известно)))