35 докзать,что если прямая перпендикулярна к одной из двух параллельных прямых то она перпендикулярна и к другой

👇

Ответ:

мирок3

28.11.2021

Доказательство: Пусть а1 и а2 - 2 параллельные прямые и плоскость, перпендикулярная прямой а1. Докажем, что эта плоскость перпендикулярна и прямой а2. Проведем через точку А2 пересечения прямой а2 с плоскостью произвольную прямую х2 в плоскости . Проведем в плоскости через точку А1 пересечения прямой а1 с прямую х1, параллельную прямой х2. Так как прямая а1 перпендикулярна плоскости , то прямые а1 и x1перпендикулярны. А по теореме 1параллельные им пересекающиеся прямые а2 и х2 тоже перпендикулярны. Таким образом, прямая а2 перпендикулярна любой прямой х2 в плоскости . А это ( по определению )значит, что прямая а2 перпендикулярна плоскости . Теорема доказана.1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

4,8(69 оценок)

Открыть все ответы

Ответ:

nafani1

28.11.2021

Решение

sin (pi/2+t)-cos(pi-t)+tg(pi-t)+ctg(5pi/2-t) = cost + cost - tgt + tgt =2cost

Объяснение:

sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t). Для упрощения данного выражения используем формулы приведения. По формулам приведения: sin (π/2 + t) = cos t; cos (π - t) = – cos t; tg (π - t) = – tg t; ctg (5π/2 - t) = tg t. Таким образом, мы пришли к выражению: cos t - (– cos t) + (– tg t) + tg t = (раскроем скобки, если перед скобками стоит знак минус "-", то знак слагаемого в скобках необходимо поменять на противоположный) = cos t + cos t - tg t + tg t = (- tg t и tg t взаимно уничтожаются) = 2cos t. ответ: sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t) = 2cos t.

4,5(75 оценок)

Ответ:

baget97ozu06u

28.11.2021

========================================================

Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

========================================================

AB = a = 45 : 3 = 15 смРадиус окружности, описанной около правильного треугольника, вычисляется через его сторону: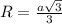 $R=\frac{a\sqrt{3}}{3}\\\\$ Радиус окружности, описанной около правильного восьмиугольника, вычисляется через его сторону: 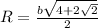$R=\frac{b\sqrt{4+2\sqrt{2}}}{2}\\\\$ Приравниваем правые части и находим искомую величину: 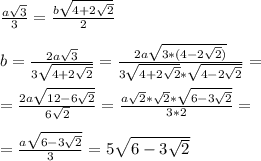$\frac{a\sqrt{3}}{3}=\frac{b\sqrt{4+2\sqrt{2}}}{2}\\\\b=\frac{2a\sqrt{3}}{3\sqrt{4+2\sqrt{2}}}=\frac{2a\sqrt{3*(4-2\sqrt{2})}}{3\sqrt{4+2\sqrt{2}}*\sqrt{4-2\sqrt{2}}}=\\\\=\frac{2a\sqrt{12-6\sqrt{2}}}{6\sqrt{2}}=\frac{a\sqrt{2}*\sqrt{2}*\sqrt{6-3\sqrt{2}}}{3*2}=\\\\=\frac{a\sqrt{6-3\sqrt{2}}}{3}=5\sqrt{6-3\sqrt{2}}\\\\$ b - сторона правильного шестиугольника b ≈ 6,63 смОТВЕТ: 5√(6 - 3√2)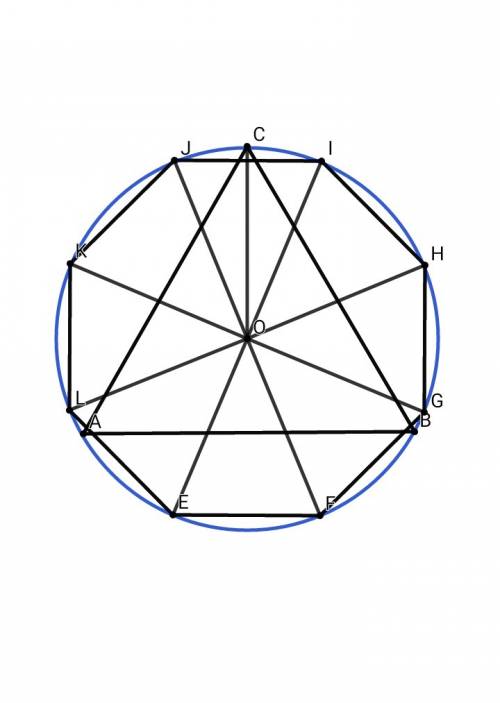
.(Периметр правильного треугольника вписанного в окружности равен 45см. найдите сторону правильного