1) Боковая поверхность цилиндра равна 2"пи"rh, где r -радиус основания, а h - высота. Объем цилиндра равен "пи"*(r^2)*h.
2) После увеличения высоты цилиндра на 4 см она будет равна (h+4) и объем такого цилиндра будет равен "пи"*(r^2)*(h+4). Новый объем больше предыдущего на
"пи"*(r^2)*(h+4)-"пи"*(r^2)*h, что равно 36"пи". Получим уравнение:
"пи"*(r^2)*(h+4)-"пи"*(r^2)*h=36"пи"; после упрощения получим 4*r^2=36; r^2=9; r=3
3) Тогда площадь боковой пов-сти цилиндра равна 2"пи" * 3 * 5 =30"пи" (см квадр.)
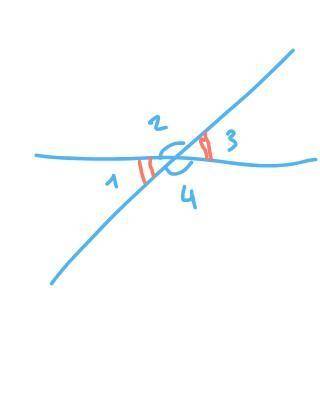
При пересечении двух прямых образуются четыре угла.
Вертикальные углы — у которых стороны одного угла являются продолжениями сторон другого угла. Вертикальные углы равны. Есть две пары вертикальных углов — ∠1 и ∠3, ∠2 и ∠4.
Смежные углы — два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой. Смежные углы в сумме равны 180°. Есть четыре пары смежных углов — ∠1 и ∠2, ∠2 и ∠3, ∠3 и ∠4, ∠1 и ∠4.
По условию, сумма трёх углов равна 196°.
∠1 + ∠2 + ∠3 = 196°.
∠1 и ∠2 — смежные углы, ∠1 + ∠2 = 180°, => ∠3 = 196° – 180° = 16°.
∠1 и ∠3 — вертикальные углы, ∠1 = ∠3 = 16°, => ∠2 = 196° – 16° – 16° = 164°.
Итого, ∠1 = ∠3 = 16°, ∠2 = ∠4 = 164°.
Меньший угол — ∠1 и ∠3 — равен 16°.
ответ: 16°.
2a² +h² = 6² ⇒ 2a² +h² = 36;
4ah=32;⇒ah=8 ⇒a²h² =64⇒ 2a²*h²=128;
обозначая 2a²=x ; h² =y получим систему
{x+y =36 ;
{xy=128 ;
x² - 36x+128=0;⇒x=4 ; 32 соответственно y= 32 ; 4.
a)
2a² =4 ⇒a² =2,
h² =32 ⇒h=4√2 ;
V=a²*h=2*4√2=8*√2;
b)
2a²=32⇒a² =16,
h² =4 ⇒ h =2;
V=a²*h=16*2 = 32 .
ответ : 8*√2 или 32.