ответ: 13,44 см
Объяснение:
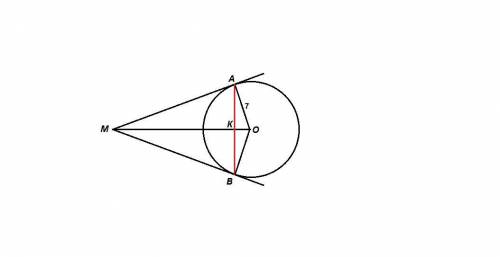
МА и МВ - касательные, точки А и В - точки касания.
MO = 25 см,
ОА = ОВ = 7 см - радиусы.
ОА⊥МА и ОВ⊥МВ как радиусы, проведенные в точку касания.
По свойству касательных, проведенных из одной точки, МА = МВ и ∠АМО = ∠ВМО.
Тогда МК - биссектриса равнобедренного треугольника МАВ, значит является и медианой и высотой, ⇒
К - середина АВ, АК⊥МО.
ΔМОА: ∠МАО = 90°, по теореме Пифагора
МА = √(МО² - ОА²) = √(25² - 7²) = √((25 - 7)(25 + 7)) =
= √(18 · 32) = √(9 · 2 · 16 · 2) = 3 · 2 · 4 = 24 см
АК - высота прямоугольного треугольника МОА.
Smoa = 1/2 MO · AK = 1/2 OA · MA
AK = OA · MA / MO = 7 · 24 / 25 = 168/25 = 6,72 см
АВ = 2 АК = 2 · 6,72 = 13,44 см
BE-высота=5см.
BC-меньшее основание, AD-большее основание.
AD-BC=16 см
2)SABCD=1/2BExADxBC
Пусть AD-X,
тогда BC-(X-16),
BE=5 см.
75=1/2x5xXx(X-16)
75=5/2X(X-16)
75=5/2X^2-40
-5/2X^2=-75-40
-5/2X^2=-115
5/2X^2=115
x^2=115x2/5=23x2=46 см
x=√46 см
ответ.AD=√46 см.