Объяснение:
Радиус окружности, описанной около треугольника ABC, равен 5. Сторона AB=5, высота BD=4. Найдите длину стороны BC.
Треугольник АВС вписан в окружность.
Сторона АВ=5 и равна радиусу этой окружности, который равен 5.
Соединив центр О окружности с концами хорды АВ, получим равносторонний треугольник АОВ.
Угол АОВ=60º
Вписанный угол ВСА равен половине центрального. опирающегося на дугу АВ.
Угол АСВ=30º
∆ ВСD- прямоугольный по условию, ВD- высота и равна 4
Катет BD противолежит углу 30º, ⇒ гипотенуза ВС треугольника ВСD равна 4*2=8.
МО = 24см
Теория:Свойство прямоугольного треугольника: катет, лежащий напротив угла 30°, равен половине гипотенузы.Теорема Пифагора: с²=а²+b². *где с - гипотенуза, а и b - катеты.Решение:Рассмотрим ∆NOK - прямоугольный (∠NKO=90°).
∠ONK = 180-(90+60) = 30°(по теореме о сумме углов треугольника).
По свойству катета, лежащего напротив угла 30°, КО=1/2*NO, отсюда NO=2КО = 24см.
По теореме Пифагора NO²=KO²+NK², отсюда NK равно:
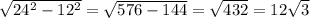
NK=(12✓3)см.
Рассмотрим ∆NМK - прямоугольный (∠NKO=90°).
По свойству катета, лежащего напротив угла 30°, NK=1/2*NM, отсюда NM = 2NK = 2*12✓3 = (24✓3)см.
По теореме Пифагора NM²=NK²+MK², отсюда MK равно:
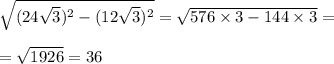
МК = 36см
МО = МК - ОК = 36-12 = 24см.
По синусу гла находим сторону СВ
cos60=DB/CB, отсюда выражаем СВ = 1/1/2=2
Теперь по теореме Пифагора найдем СD^2=2^2-1^2=3
СD=корень из 3
Теперь по пропорциоальным отрезкам в прямоугольном треугольнике находим гипотенузу треугольника АВС
CD^2=AD*DB
(корень из 3)^2=AD*1
AD=3
Гипотенуза АВ=3+1=4 см