Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Осноположником геометрии можно считать Евклида. В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». В развитии Геометрия можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.
Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Геометрия, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.Геоме́трия (от др. ... γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.
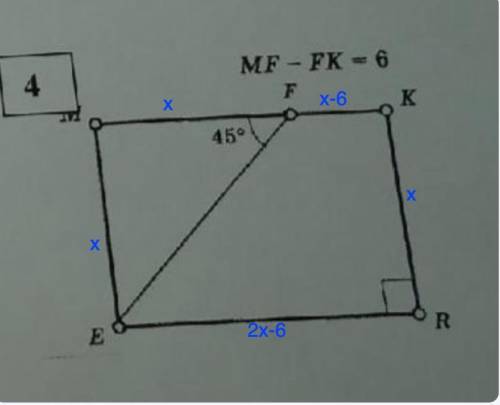
EM=KR=8; MK=ER=10
Объяснение:
Дано: ЕМКR - прямоугольник
∠MFE=45°
MF-FK=6
P (ЕМКR)=36
Найти: стороны прямоугольника.
Пусть MF=x ⇒ FK=MF-6=x-6
Рассмотрим ΔEMF - прямоугольный
∠MFE=45°
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠MEF=45°
ΔEMF - равнобедренный (углы при основании равны)
⇒ EM=MF=x
Противоположные стороны прямоугольника равны.
EM=KR=x
MK=ER=x+(x-6)=2x-6
Периметр прямоугольника равен удвоенной сумме длин соседних сторон.
Р (ЕМКR)=2(х+2х-6)=2(3х-6)
36=2(3х-6)
3х-6=18
3х=24
х=8
⇒ EM=KR=8
MK=ER=2x-6=10