1)
Диаметр вписанного в куб шара равен длине ребра куба, а радиус - половине длины ребра.
Площадь полной поверхности куба равна сумме площадей его 6-ти граней.
Площадь одной грани равна а² =1170/π :6=195/π
R²= (a/2)²=195/4π
Из формулы площади поверхности шара
S=4πR²=4π•195/4π=195 (ед. площади)
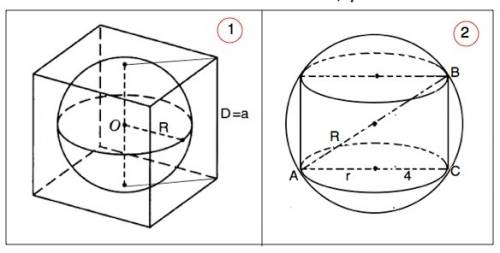
2)
Окружности, ограничивающие основания вписанного цилиндра изнутри касаются шара.
Осевое сечение цилиндра - прямоугольник, проходит через центр шара, при этом диаметр шара является диагональю этого прямоугольника.
Из формулы площади поверхности сферы 4πR²=100π находим её радиус R=5 ⇒ D=10
Диаметр основания цилиндра d=2r=8.
Из прямоугольного ∆ АВС высота ( образующая) цилинда ВС=6 ( по т.Пифагора или обратив внимание на отношение катета АС и гипотенузы АВ 4:5 - отношение сторон "египетского" треугольника)
Высота цилиндра - 6 ед. длины.
ответ: площадь трапеции 50 см²
Объяснение: для нахождения площади трапеции нам не известна ее высота. Известно, что угол между основанием и боковой стороной образует угол 30°. При проведении высоты образуется прямоугольный треугольник с гипотенузой 8 см и катетом, лежащим против угла 30°. Этот катет и будет высотой трапеции. Найдем высоту трапеции, она будет равна половине гипотенузы, т.е. 10:2=5 см. Теперь найдем площадь трапеции: она равна половине суммы оснований умноженных на высоту: (8+12):2х5=50см²