Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
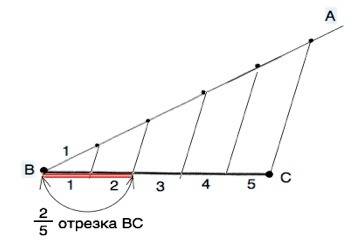
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
Векторы, лежащие на параллельных прямых, называются коллинеарными. Пусть векторы А и В коллинеарны и не равны нулю. Параллельным переносом вектора А можно начало А совместить с началом В. Если кроме общего начала векторы А и В не имеют других общих точек, то эти векторы противоположно направлены ("смотрят в разные стороны"), а в противном случае эти векторы сонаправлены, или одинаково направлены ("смотрят в одну сторону").