Задача 1.
S=kh
Соответственно k=S:h
60:12=5 - средняя линия трапеции
Задача 2.Площадь трапеции вычисляется по формуле a+b/2*h подставляем известные нам значения в формулу получаем 8*(8+b/2)=72
=128+b=144
b=16
Задача 3.
S=kh
Соответственно k=S:h
63:7=9 - средняя линия трапеции
Задача 4.
12*1+b/2=60
1+b=5
b=4
Задача 5
рассмотрим треугольник, образованный высотой, опущенной на основание и наклонной боковой стороной. Он прямоугольный и равнобедренный. Значит высота трапеции равна разнице между основаниями 9-5=4
площадь равна высоте умноженной на полусумму оснований 4 * (9+5)/2 =28
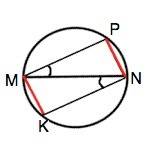
Вписанные углы РMN и KNM опираются на равные хорды. Следовательно, дуги, стягиваемые этим хордами, равны. Вписанные углы, опирающиеся на равные дуги (или на равные хорды), равны.
∠РMN=∠KNM
Проведем хорды МР и КN.
В треугольниках MPN и MKN вписанные ∠Р = ∠К (опираются на диаметр).⇒
Прямоугольные ∆ МРN=∆ MKN по острому углу и общей гипотенузе.
Отсюда следует равенство PNM=KMN
Эти углы - накрестлежащие при пересечении РN и MK секущей MN.
Если при пересечении двух прямых секущей накрестлежащие углы равны. эти прямые - параллельны. Доказано.
AH=1/2*3(корень из 3)=1,5(корень из 3);
По т. Пифагора:
AB^2=AH^2+BH^2;
BH= корень(3(корень из 3)^2-1,5(корень из 3)^2)=корень(27-6,75)=корень(20,25)=4,5
ответ: BH=4.5