Единичный тетраэдр - треугольная пирамида, длина каждого ребра которой равна единице. Следовательно, пирамида МАВС - правильная, все ее грани - правильные треугольники.
Данное сечение - треугольник, высота которого равна высоте МО пирамиды, а основание - высоте АН основания пирамиды.
Основание О высоты правильной пирамиды - точка пересечения высот ( медиан, биссектрис) основания АВС.
АО=радиусу описанной окружности.
АО=R=a/√3=1/√3 (по формуле радиуса описанной окружности).
По т.Пифагора из ∆ АМО высота
МО=√(AM²-AO²)=√(1-1/3)= \sqrt{ \frac{2}{3}
S ∆ MAH= MO•AH:2 =\sqrt{2}: {4}
2
:4
Объяснение:
держи)
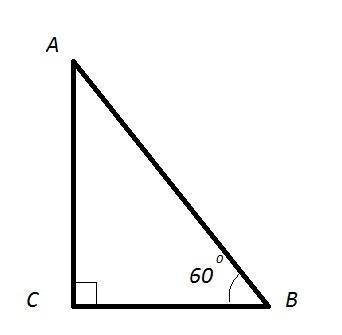
ΔАСВ - прямоугольный : АВ - гипотенуза ; АС,СВ - катеты
∠С= 90°
∠В = 60°
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно: ∠А = 90 - 60 = 30°
Катет лежащий против угла в 30° равен половине гипотенузы.
СВ = АВ/2
По теореме Пифагора:
АВ² = АС² + СВ² ⇒ АВ² = АС² + (АВ/2)²
АС= √ (АВ² - (АВ²/4)) ⇒ АС = √ ((4АВ² - АВ²)/4) = √(3АВ²/4) = (АВ*√3) /2
S =1/2 * АС * СВ = 18√3 / 3
1/2 * ((АВ*√3)/2 * (АВ/2)) = 18√3 / 3
1/2 * ( (АВ²*√3) / 4 ) = 18√3 / 3
АВ²√3 / 8 = 18√3 / 3
3 *√3* АВ² = 18√3 * 8
АВ² = 144√3 / 3√3
АВ² = 48
АВ = √48 = √(16*3) = 4√3 - гипотенуза
СВ = 4√3 /2 = 2√3 - один катет
АС = (4√3 *√ 3)/2 = (4*(√3)²)/2 = 12/2 = 6 - второй катет, который лежит против угла В = 60°.
ответ: АС = 6.
15:2=7,5(см) - середина крайнього відрізка
7,5+15+15+7,5=45(см) - відстань між серединами отриманих крайніх відрізків.