1) Боковое ребро образует с плоскостью основания угол 45 градусов следовательно угол АВС(обозначимего так, угол которойнаверху) тоже равен 45 градусов. Следовательно, ВЫСОТА пирамиды=Радиус описанной окружности.
2)Обозначим ВЫСОТУ=РАДИУС ОПИС.ОКР. через х. По т.Пифагора найдем х:
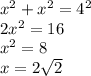
ВЫСОТА=РАДИУС.ОПИС.Окр.=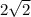
3) Радиус описанной окружности = диагональ квадрата разделить на 2 (В основании квадрат т.к. пирамида 4-х угольная и правильная)
Отсюда, диагональ квадрата = 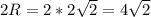
4)Сторона квадрата=диагональ кв. делить на корень из 2= 4см
5)Площадь основания = сторона в квадрате=16 см^2
6)бок.поверхн-ть = 1/2 * Периметр основания * высота = 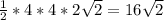
7)Площадь полной поверхности=16+16 кореньиз 2
a) Равные отрезки по осям - треугольник равносторонний.
b) По разности координат находим длины сторон треугольника.
А(2; 0; 5), В(3; 4; 0), С(2; 4; 0)
Квадрат Сторона
AB = √((xB-xA)²+(yB-yA)²+(zB-zA)²) = 1 16 25 42 6,480740698
BC = √((xC-xB)²+(yC-yB)²+(zC-zB)²) = 1 0 0 1 1
AC = √((xC-xA)²+(yC-yA)²+(zC-zA)²) = 0 16 25 41 6,403124237 .
По теореме косинусов находим углы:
Полупериметр р= 6,941932468 .
cos A = 0,98802352 cos B = 0,15430335 cos C = 0
A = 0,15492232 В = 1,415874007 С = 1,570796327 это радианы
8,876395081 81,12360492 90 это градусы.
Треугольник прямоугольный.
Можно было определить и по сумме квадратов сторон:
ВС^2 + AC^2 = AB^2.