Согласно теореме синусов
AB / sin C = BC / sin A , откуда
BC = AB * sin A / sin C = 8 * sin 45° / sin 30° = 8 * √2/2 / 1/2 = 8 * √ 2 см.
а) Координаты середины отрезка равны полусуммам соответствующих координат его концов.
А (2; -1; 0), В (-4; 2; 2)
Обозначим середину отрезка АВ буковой К
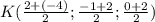
К (-1; 0,5; 1)
б) Нужно найти координаты точки С, если точка В является серединой отрезка АС. Координаты точек А и В известны. Координаты точки С обозначим (x; y; z). И используем формулу для нахождения координат середины отрезка. Находим координаты середины отрезка АС.
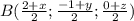
Координаты точки В известны. Приравняем их и получим три уравнения, решая которые найдем координаты точки С.
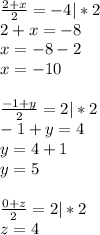
C (-10; 5; 4)
в) Длина отрезка можно вычислить так: квадратный корень из суммы квадратов разностей соответствующих координат концов отрезка.
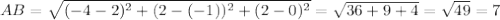
АВ=7
1) Удалите номера неверных утверждений:
1. Если один из острых углов прямоугольного треугольника равен 73о, то второй острый угол равен 27о. - неверно, 17°
2. Если углы при основании равнобедренного треугольника равны по 60о, то такой треугольник – правильный. - верно, третий угол тоже 60°
3. Существует треугольник со сторонами 3,4,5. - существует, это прямоугольный треугольник, "египетский"
2) Удалите номер верных утверждений:
1. Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие треугольники равны. - верно
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180о. - верно
3. Если в треугольнике два угла равны, то он равнобедренный. - верно
3) Сформулируйте теорему о катете прямоугольного треугольника, лежащего против угла в 30 градусов. - Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
4) Острые углы прямоугольного треугольника относятся как 12:18. Найдите эти углы.
Сумма острых углов прямоугольного треугольника составляет 90 градусов. Пусть ∠1=12х°, ∠2=18х°, тогда 12х+18х=90; 30х=90; х=3.
∠1=12*3=36°; ∠2=18*3=54°
ответ: 36°, 54°
Пусть имеем треугольник ABC, по теореме синусов
AB/sin(ACB) =BC/sin(CAB)
8/sin(30) =BC/sin(45)
8/0,5=BC/(1/sqrt(2))
BC=16/sqrt(2)=8*sqrt(2)
ответ:A)