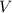призмы = 
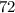см³.
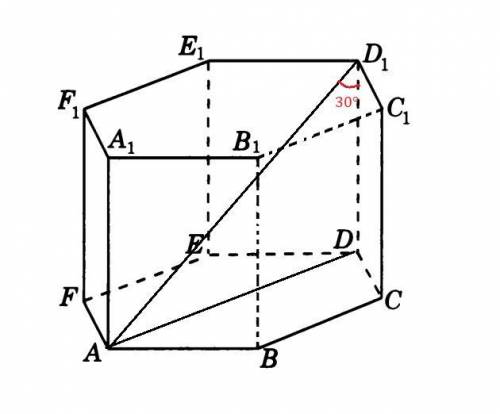
Обозначим данную призму буквами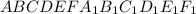 
.
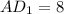см.
============================================================
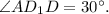
Если призма правильная, то она всегда будет прямой.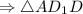
- прямоугольный, где 
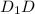- высота данной призмы.
Рассмотрим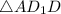 
:
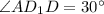, по условию.
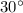, то напротив лежащий катет равен половине гипотенузы.
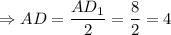см.
По теореме Пифагора найдём высоту :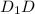
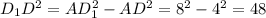
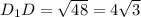см.
Рассмотрим нижнее основание данной призмы:
шестиугольник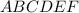 
- правильный, так как данная призма тоже правильная.
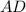- большая диагональ шестиугольника .
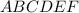По свойству правильного шестиугольника,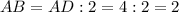 
см.
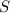шестиугольника = 
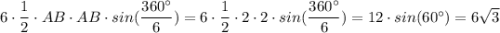cм².
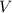призмы = 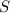шестиугольника
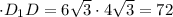см³
Пусть АЕ=х, тогда FD=(AD-BC)-x или FD=12-x.
Из треугольников АВЕ и CDF выразим по Пифагору h²:
h²=AB²-AE² и h²=CD²-(12-x)². Приравняем оба выражения:
AB²-AE²=CD²-(12-x)². Подставив известные значения и раскрыв скобки,
найдем х: х=12см.
Тогда h=√(AB²-AE²) =√(400-144) = 16cм.
Площадь трапеции равна произведению полусуммы оснований на высоту, то есть [(5+17):2]*16 = 11*16=176см².
ответ: Sт=176см².